题目内容
如图,甲、乙、丙、丁四个图都称作平面图,观察图甲和表中对应数值,探究计数的方法并作答.

(1)数一数每个图各有多少个顶点,多少条边,这些边围出多少区域,并将结果填入下表.
(2)根据表中数值,写出平面图的顶点数m,边数n、区域数f之间的一种关系:
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)题中得出的关系,则这个平面图有

(1)数一数每个图各有多少个顶点,多少条边,这些边围出多少区域,并将结果填入下表.
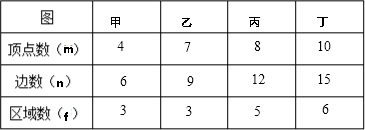
| 图 | 甲 | 乙 | 丙 | 丁 |
| 顶点数m | 4 | 7 | ||
| 边数n | 6 | 9 | ||
| 区域数f | 3 |
m+f=n+1
m+f=n+1
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)题中得出的关系,则这个平面图有
30
30
条边.分析:(1)按照自己熟悉的规律去数顶点数,边数以及区域数;
(2)4+3-6=1,7+3-9=1,8+5-12=1,10+6-15=1,所以可得到一般规律:顶点数+区域数-边数=1;
(3)边数=顶点数+区域数-1.
(2)4+3-6=1,7+3-9=1,8+5-12=1,10+6-15=1,所以可得到一般规律:顶点数+区域数-边数=1;
(3)边数=顶点数+区域数-1.
解答:解:(1)结和图形我们可以得出:
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.
(2)根据以上数据,顶点用m表示,边数用n表
示,区域用f表示,他们的关系可表示为:m+f=n+1;
(3)把m=20,f=11代入上式得:n=m+f-1=20+11-1=30.
故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
故答案为:m+f=n+1;30.
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.

(2)根据以上数据,顶点用m表示,边数用n表
示,区域用f表示,他们的关系可表示为:m+f=n+1;
(3)把m=20,f=11代入上式得:n=m+f-1=20+11-1=30.
故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
故答案为:m+f=n+1;30.
点评:本题考查学生的观察能力,分析以及合理推理能力.注意应按平面图来进行解答.

练习册系列答案
相关题目
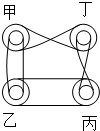 如图,甲、乙、丙、丁四个轮子连在一组皮带上,已知甲的转向为顺时针,则丙的转向为( )
如图,甲、乙、丙、丁四个轮子连在一组皮带上,已知甲的转向为顺时针,则丙的转向为( )| A、顺时针 | B、逆时针 | C、先顺后逆 | D、不能确定 |
 如图,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知,甲乙丙丁四个长方形面积和是32cm2,四边形ABCD的面积是20cm2.求甲、乙、丙、丁四个长方形周长的总和是多少厘米.
如图,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知,甲乙丙丁四个长方形面积和是32cm2,四边形ABCD的面积是20cm2.求甲、乙、丙、丁四个长方形周长的总和是多少厘米.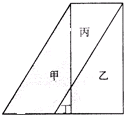 如图,甲、乙、丙、丁分别表示直角梯形中的四个部分的面积,甲与丙拼成的是平行四边形,下列等式中正确的是( )
如图,甲、乙、丙、丁分别表示直角梯形中的四个部分的面积,甲与丙拼成的是平行四边形,下列等式中正确的是( )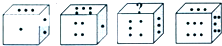 (2013?福田区模拟)如图是甲、乙、丙、丁四粒筛子,你能根据各粒显示的点数推出第三粒上面的“?”号是几点吗?
(2013?福田区模拟)如图是甲、乙、丙、丁四粒筛子,你能根据各粒显示的点数推出第三粒上面的“?”号是几点吗?