题目内容
某校六年级三个班的人数相等,一班的男生和二班的女生相等,三班的男生是全部男生的
,那么,全部女生人数与全年级人数的比是( )
| 2 |
| 5 |
分析:由“三个班人数相等,一班男生数与二班女生数相等”知,一班女生数等于二班男生数,因此一、二班男生人数的和都可表示每个班的人数,又“三班的男生人数是全部男生人数的
”,如果三班的男生人数设一个具体数值,那么就可依次求出全部男生人数以及一、二班男生人数的和(即每班人数),问题就迎刃而解了.
| 2 |
| 5 |
解答:解:设三班男人数为20人,则全部男生人数为:
20÷
=50(人)
每个班的人数为:50×(1-
)=30(人);
全部男生人数占全级人数的:50÷(30×3)=
;
全部女生占全级人数的:1-
=
;
也就是说全部女生人数与全年级人数的比是4:9.
答:全部女生人数与全年级人数的比是4:9.
故选:D.
20÷
| 2 |
| 5 |
每个班的人数为:50×(1-
| 2 |
| 5 |
全部男生人数占全级人数的:50÷(30×3)=
| 5 |
| 9 |
全部女生占全级人数的:1-
| 5 |
| 9 |
| 4 |
| 9 |
也就是说全部女生人数与全年级人数的比是4:9.
答:全部女生人数与全年级人数的比是4:9.
故选:D.
点评:在上面的例题中,将假设的数值代入解题过程,便得到正确答案.对于这类题目,假设不同的数值,都会得到相同的答案.还有一类题目,也可以使用数值代入法,但因为题中涉及的量不仅仅是倍数关系,所以假设的数不同,结果就不同,需要通过比较所得结果与已知结果来修正假设的数,从而得出正确解答.

练习册系列答案
相关题目
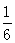 ,
,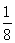 ,六(3)班占
,六(3)班占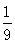 ,六年级共有多少人?
,六年级共有多少人?