题目内容
14.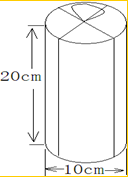 用塑料绳捆扎一个圆柱形的礼盒(如图),打结处刚好是底面的圆心,打结处绳长25厘米.
用塑料绳捆扎一个圆柱形的礼盒(如图),打结处刚好是底面的圆心,打结处绳长25厘米.(1)在它的整个侧面贴上商标,这部分的面积是多少平方厘米?
(2)做这个礼品盒至少用多少平方厘米的纸板?
(3)这个礼盒的体积是多少立方厘米?
(4)捆扎这个礼品盒共用去塑料绳多少厘米?
分析 (1)在它的整个侧面贴上商标,要贴的部分是圆柱的侧面,根据侧面积=底面周长×高可求出这部分的面积;
(2)做这个礼品盒至少用多少平方厘米的纸板,是求的圆柱的表面积,用侧面积加上2个底面积即可;
(3)根据圆柱的体积公式:V=sh可求出圆柱的体积;
(4)用塑料绳的长度是4条高,4条直径的和再加上打结外绳子的长度,据此解答.
解答 解:(1)3.14×10×20=942(平方厘米)
答:这部分的面积是942平方厘米.
(2)942+3.14×(10÷2)2×2
=942+3.14×25×2
=942+157
=1099(平方厘米)
答:做这个礼品盒至少用1099平方厘米的纸板.
(3)3.14×(10÷2)2×20
=3.14×25×20
=1570(立方厘米)
答:这个礼盒的体积是1570立方厘米.
(4)4×20+4×10+25
=80+40+25
=145(厘米)
答:捆扎这个礼品盒共用去塑料绳145厘米.
点评 本题主要考查了学生对圆柱的体积、侧面积和表面积计算方法的掌握.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
9.脱式计算
| 3.6-2.8+3.4-7.2 | 7.2×[(7.8+$\frac{1}{5}$)÷0.4] | (6.9-3.15)÷0.3×0.8 |
| $\frac{17}{23}$×2$\frac{1}{3}$+2$\frac{1}{3}$×$\frac{6}{23}$ | 3.5×2.8+5.5×2.8+2.8 | ($\frac{1}{15}$-$\frac{1}{51}$)×17×5 |
3.统计.
为了了解交通情况,小青和他的小伙伴在学校附近的十字路口统计7:20-7:30与10:00-10:10两个时段内各种车辆通过的数量,制成统计表如下:
(1)该路口7:20-7:30这10分钟内共通过109车辆.
(2)10:00-10:10这个时段内,通过该路口的小汽车车最多,大客车车最少.
(3)10:00-10:1010:00-10:10这个时段内平均1分钟有10.8辆车通过该路口.
为了了解交通情况,小青和他的小伙伴在学校附近的十字路口统计7:20-7:30与10:00-10:10两个时段内各种车辆通过的数量,制成统计表如下:
| 车型 时间段 | 小汽车 | 大卡车 | 大客车 | 摩托车 | 合计 |
| 7:20-7:30 | 35 | 17 | 8 | 49 | 109 |
| 10:00-10:10 | 42 | 23 | 11 | 32 | 108 |
(2)10:00-10:10这个时段内,通过该路口的小汽车车最多,大客车车最少.
(3)10:00-10:1010:00-10:10这个时段内平均1分钟有10.8辆车通过该路口.
4.某洗涤剂厂2000年各季度的产值如下表.(单位:万元)
根据表中数据算一算:
(1)4个季度的平均产值是1337.5万元.
(2)三季度比二季度增长12%.
| 季 度 | 一 | 二 | 三 | 四 |
| 产 值 | 1200 | 1250 | 1400 | 1500 |
(1)4个季度的平均产值是1337.5万元.
(2)三季度比二季度增长12%.