题目内容
 如图,一块长方形菜地,长与宽的比是5:3,在修整时长和宽都增加5米,结果面积增加了345平方米(阴影部分).求原来菜地的面积是多少平方米?
如图,一块长方形菜地,长与宽的比是5:3,在修整时长和宽都增加5米,结果面积增加了345平方米(阴影部分).求原来菜地的面积是多少平方米?分析:设原来长方形菜地的长为a米,宽为b米,因此阴影部分的面积可以分割成长宽分别为a米和5米以及b米和5米的两个长方形的面积与一个边长为5米的正方形的面积之和,由阴影部分的面积已知可以列出方程5a+5b+5×5=345,由此可求得a+b的值,即原长方形的长宽之和,再根据“长与宽的比是5:3”,即可求得原长方形的长与宽,进而求得面积.
解答:解:设原来长方形菜地的长为a米,宽为b米,由题意可得,
5a+5b+5×5=345
5a+5b=320
a+b=64,
因为长与宽的比是5:3,
所以长为
×64=40(米),
宽为
×64=24(米),
40×24=960(平方米).
答:原来菜地的面积是960平方米.
5a+5b+5×5=345
5a+5b=320
a+b=64,
因为长与宽的比是5:3,
所以长为
| 5 |
| 5+3 |
宽为
| 3 |
| 5+3 |
40×24=960(平方米).
答:原来菜地的面积是960平方米.
点评:本题解决的关键是根据阴影部分的面积求得原长方形的长与宽的和,进而根据长宽的比求得长与宽.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
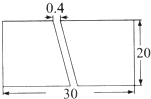 如图,一块长方形菜地中有一条等宽的小路(即小路的两边互相平行),请你根据图中数据计算小路的占地面积.(单位:m)
如图,一块长方形菜地中有一条等宽的小路(即小路的两边互相平行),请你根据图中数据计算小路的占地面积.(单位:m) (2010?武陵区)如图,一块长方形菜地的长是9米,宽为4米,在长方形菜地长边的中点P处有一口井,现把这块菜地平均分给4家,使这4家共用这口井,可以按如图分法.(其中E为AD的中点)每家可分得9平方米的地.
(2010?武陵区)如图,一块长方形菜地的长是9米,宽为4米,在长方形菜地长边的中点P处有一口井,现把这块菜地平均分给4家,使这4家共用这口井,可以按如图分法.(其中E为AD的中点)每家可分得9平方米的地.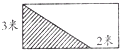 如图.一块长方形菜地的面积是24平方米,阴影部分的面积是多少平方米?
如图.一块长方形菜地的面积是24平方米,阴影部分的面积是多少平方米? 如图是一块长方形菜地,长900m,宽400m.在长方形长边的中点A处有一口井,现要把这块菜地平均分给3户人家,且使3家的地都与井口相邻,怎样分?请画出示意图,并说明理由.
如图是一块长方形菜地,长900m,宽400m.在长方形长边的中点A处有一口井,现要把这块菜地平均分给3户人家,且使3家的地都与井口相邻,怎样分?请画出示意图,并说明理由.