题目内容
12.△ABC中,AE=$\frac{2}{5}$AC,BD=$\frac{1}{6}$BC,阴影部分面积是三角形ABC面积的$\frac{{({\;}\right.\left.{\;})}}{{({\;}\right.\left.{\;})}}$.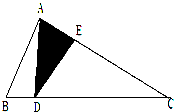
分析 设阴影部分面积是1,因为AE=$\frac{2}{5}$AC,又因为等高的三角形,面积比等于底边的长度比,所以三角形ACD面积=1÷$\frac{2}{5}$=$\frac{5}{2}$;同理,又因为BD=$\frac{1}{6}$BC,则三角形ABC面积=$\frac{5}{2}$÷$\frac{6-1}{6}$=3;然后根据除法的意义,用阴影部分的面积除以三角形ABC的面积即可.
解答 解:设阴影部分面积是1,因为AE=$\frac{2}{5}$AC,所以三角形ACD面积=1÷$\frac{2}{5}$=$\frac{5}{2}$;
同理,又因为BD=$\frac{1}{6}$BC,则三角形ABC面积=$\frac{5}{2}$÷$\frac{6-1}{6}$=3;
阴影部分面积是三角形ABC面积的:1÷3=$\frac{1}{3}$.
答:阴影部分面积是三角形ABC面积的$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了三角形的面积与底的正比关系,关键是明确等高的三角形,面积比等于底边的长度比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.要反映济宁市2013年各月份平均气温变化情况,用( )统计图比较合适.
| A. | 扇形 | B. | 条形 | C. | 折线 |
