题目内容
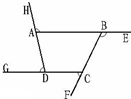如图，将四边形ABCD的四条边分别延长一段，得∠CBE、∠BAH、∠ADG、∠DCF，那么，这四个角的和等于360°
360°
．分析：根据平角的定义，可以得出∠CBE+∠1=∠BAH+∠2=∠ADG+∠3=∠DCF+∠4=180°，又因为四边形的内角和是360°，所以可得：∠1+∠2+∠3+∠4=360°，由此利用代换的思想即可计算得出∠CBE、∠BAH、∠ADG、∠DCF，这四个角的和．
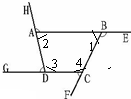
解答：解：根据题干分析可得：
∠CBE+∠1+∠BAH+∠2+∠ADG+∠3+∠DCF+∠4=180°×4=720°，
又因为：∠1+∠2+∠3+∠4=360°（四边形内角和定理），
所以∠CBE+∠BAH+∠ADG+∠DCF=720°-（∠1+∠2+∠3+∠4）=720°-360°=360°，
答：这四个角的度数之和是360°．
故答案为：360°．
∠CBE+∠1+∠BAH+∠2+∠ADG+∠3+∠DCF+∠4=180°×4=720°，
又因为：∠1+∠2+∠3+∠4=360°（四边形内角和定理），
所以∠CBE+∠BAH+∠ADG+∠DCF=720°-（∠1+∠2+∠3+∠4）=720°-360°=360°，
答：这四个角的度数之和是360°．
故答案为：360°．
点评：此题考查了利用平角的定义和四边形内角和定理证明四边形的外角和是360°的推理方法．
练习册系列答案
名校课堂系列答案
相关题目
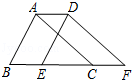如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（ ）
如图，在直角三角形ABC中，∠ACB=90°，AC=BC=10，将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1．