题目内容
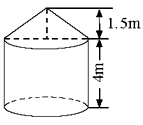
一个稻谷上面是圆锥形，下面是圆柱形，圆柱的底面周长是18.84米，高是2米，圆锥的高是1.5米，每立方米稻谷约重550千克，这囤稻谷约有多少吨？（得数保留整数）
分析：首先求这个粮囤的体积，根据圆锥与圆柱的体积公式；然后求这个粮囤最多能装稻谷多少吨，用求得的粮囤的体积，乘单位体积的稻谷的重量即可．
解答：解：圆柱的底面积为：
3.14×（18.84÷3.14÷2）2，
=3.14×32，
=3.14×9，
=28.26（平方米）；
这个粮囤的体积：
×28.26×1.5+28.26×2，
=28.26×2.5，
=70.65（立方米）；
70.65×550=38857.5（千克），
38857.5千克=38.8575吨；
答：这个粮囤最多能装稻谷38.8575吨．
3.14×（18.84÷3.14÷2）2，
=3.14×32，
=3.14×9，
=28.26（平方米）；
这个粮囤的体积：
| 1 |
| 3 |
=28.26×2.5，
=70.65（立方米）；
70.65×550=38857.5（千克），
38857.5千克=38.8575吨；
答：这个粮囤最多能装稻谷38.8575吨．
点评：此题主要考查学生对圆锥与圆柱的体积公式的掌握与运用．
练习册系列答案
相关题目
（2013?福田区模拟）一个装满稻谷的粮囤，上面是圆锥形，下面是圆柱形（如图）．量得圆柱底面的周长是62.8米，高2米，圆锥的高是1.2米．这个粮囤能装稻谷多少立方米？如果每立方米稻谷重500千克，这个粮囤最多能装稻谷多少吨？（保留一位小数）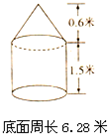
小华家有一个谷囤（如图），下面是圆柱形，上面是圆锥形．
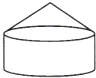一个谷囤的形状如图，下面是圆柱形，底面周长是18.84米，高是2米；上面是圆锥形，高是1.5米．这个谷囤最多能装稻谷多少立方米？