题目内容
 用一些边长1厘米的小正方形拼成一排,可以得到一个长方形(如图).
用一些边长1厘米的小正方形拼成一排,可以得到一个长方形(如图).
(1)观察上面的图形,完成下表.
(2)计算当n=20时,所拼成的长方形的周长是多少厘米.
| 正方形的个数 | 1 | 2 | 3 | 4 | 5 | … | n |
| 长方形的周长 | 4 | 6 | 8 | … |
解:(1)由图可知,每多一个小正方形,周长就增加2厘米,一个正方形的周长是4厘米,
两个正方形拼成一行的周长是4+2×1=6厘米,
三个正方形拼成一行的周长就是4+2×2=8厘米,
四个正方形拼成一行的周长就是4+2×3=10厘米,
五个正方形拼成一行的周长就是4+2×4=12厘米,
依次类推,拼成一行的桌子数为n时,能坐4+2(n-1)=2n+2人.
由此完成表格如下所示:
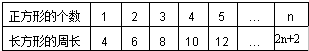
(2)当n=20时,2n+2=2×20+2=42(厘米),
答:此时所拼成的长方形的周长是42厘米.
分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
两个正方形拼成一行的周长是4+2×1=6厘米,
三个正方形拼成一行的周长就是4+2×2=8厘米,
四个正方形拼成一行的周长就是4+2×3=10厘米,
五个正方形拼成一行的周长就是4+2×4=12厘米,
依次类推,拼成一行的桌子数为n时,能坐4+2(n-1)=2n+2人.
由此完成表格如下所示:
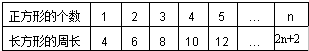
(2)当n=20时,2n+2=2×20+2=42(厘米),
答:此时所拼成的长方形的周长是42厘米.
分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
相关题目
 (2004?滨湖区)用一些边长1厘米的小正方形拼成一排,可以得到一个长方形(如图).
(2004?滨湖区)用一些边长1厘米的小正方形拼成一排,可以得到一个长方形(如图).