题目内容
求出下列各组数的最大公约数和最小公倍数
39和13
7和13
48和84.
解:(1)39和13是倍数关系,13是较小数,39是较大数,
所以它们的最大公因数是13,最小公倍数是39;
(2)7和13是互质数,
所以它们的最大公因数是1,最小公倍数是它们的乘积:7×13=91;
(3)48=2×2×2×2×3,
84=2×2×3×7,
所以48和84的最大公因数是2×2×3=12,
最小公倍数是:2×2×3×2×2×7=336.
分析:(1)39和13是倍数关系,倍数关系的两个数的最大公约数是较小数,最小公倍数是较大数,据此解答;
(2)7和13是互质数,互质数的最大公因数是1,最小公倍数是它们的乘积,据此解答;
(3)最大公约数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此把48和84分解质因数,然后据此求出.
点评:本题主要考查两个数的最大公因数和最小公倍数的求法,注意分清两个数的关系,掌握倍数关系和互质数的最大公因数和最小公倍数的求法.
所以它们的最大公因数是13,最小公倍数是39;
(2)7和13是互质数,
所以它们的最大公因数是1,最小公倍数是它们的乘积:7×13=91;
(3)48=2×2×2×2×3,
84=2×2×3×7,
所以48和84的最大公因数是2×2×3=12,
最小公倍数是:2×2×3×2×2×7=336.
分析:(1)39和13是倍数关系,倍数关系的两个数的最大公约数是较小数,最小公倍数是较大数,据此解答;
(2)7和13是互质数,互质数的最大公因数是1,最小公倍数是它们的乘积,据此解答;
(3)最大公约数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此把48和84分解质因数,然后据此求出.
点评:本题主要考查两个数的最大公因数和最小公倍数的求法,注意分清两个数的关系,掌握倍数关系和互质数的最大公因数和最小公倍数的求法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
求未知数x.
| 3.2x-4×3=52 | 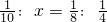 | 5x-2x=12 |
竖式计算,带*的要验算.
| *782+645= | *700-258 | 76÷9= | 50÷8= |
| 408×7= | 588×4= | 600×6 | 450×8. |
 a=
a= b,a和b的最简整数比是________.
b,a和b的最简整数比是________.