题目内容
 如图平行四边形中,甲的面积是48平方厘米,乙的面积占平行四边形的
如图平行四边形中,甲的面积是48平方厘米,乙的面积占平行四边形的| 1 | 5 |
80
80
平方厘米.分析:根据图示,以及三角形面积公式可得:丙的面积=甲的面积+乙的面积,设平行四边形的面积是x,那么乙的面积就是
x,丙的面积=四边形面积-甲的面积-乙的面积,也就是x-48-
x=
x-48,再根据丙的面积=甲的面积+乙的面积,可列方程:48+
x=
x-48,依据等式的性质,求出x的值,再代入丙的面积即可解答.
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
解答:解:设平行四边形的面积是x,
丙的面积:
x-48-
x,
=
x-48,
48+
x=
x-48,
48+
x-
x=
x-48-
x,
48+48=
x-48+48,
x=96,
x÷
=96÷
,
x=160,
×160-48,
=128-48,
=80(平方厘米),
答:丙的面积是80平方厘米,
故答案为:80.
丙的面积:
x-48-
| 1 |
| 5 |
=
| 4 |
| 5 |
48+
| 1 |
| 5 |
| 4 |
| 5 |
48+
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
48+48=
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
x=160,
| 4 |
| 5 |
=128-48,
=80(平方厘米),
答:丙的面积是80平方厘米,
故答案为:80.
点评:解答本题的关键是:明确丙的面积=甲的面积+乙的面积,用x分别表示出乙和丙的面积.

练习册系列答案
相关题目
 (2012?石狮市模拟)如图,在平行四边形中,甲的面积是36平方厘米,乙的面积是63平方厘米,则丙的面积是
(2012?石狮市模拟)如图,在平行四边形中,甲的面积是36平方厘米,乙的面积是63平方厘米,则丙的面积是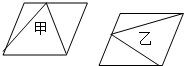 如图两个完全相同的平行四边形中,甲的面积( )乙的面积.
如图两个完全相同的平行四边形中,甲的面积( )乙的面积. 如图平行四边形中,丙的面积是60平方厘米,乙的面积占平行四边形的
如图平行四边形中,丙的面积是60平方厘米,乙的面积占平行四边形的 如图平行四边形中,丙的面积是60平方厘米,乙的面积占平行四边形的
如图平行四边形中,丙的面积是60平方厘米,乙的面积占平行四边形的 ,乙的面积是________平方厘米.甲的面积是________平方厘米.
,乙的面积是________平方厘米.甲的面积是________平方厘米.