题目内容
如图ABCD是正方形,E、F分别是AB、BC中点,阴影部分的面积占正方形的几分之几?
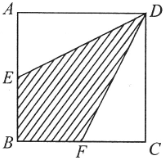

分析:如下图:连接BD,已知E、F分别是AB、BC中点,所以BF=FC,AE=EB,等底等高的三角形的面积相等,所以△ADE=△EDB=△BDF=△FCD,故阴影部分的面积占正方形的
.
| 1 |
| 2 |
解答:解:如图:
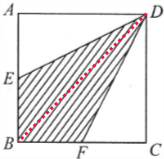
连接BD,已知E、F分别是AB、BC中点,所以BF=FC,AE=EB,
等底等高的三角形的面积相等,
所以△ADE=△EDB=△BDF=△FCD,
故阴影部分的面积占正方形的
.
答:阴影部分的面积占正方形的
.

连接BD,已知E、F分别是AB、BC中点,所以BF=FC,AE=EB,
等底等高的三角形的面积相等,
所以△ADE=△EDB=△BDF=△FCD,
故阴影部分的面积占正方形的
| 1 |
| 2 |
答:阴影部分的面积占正方形的
| 1 |
| 2 |
点评:此题解答关键是明确:等底等高的三角形的面积相等.

练习册系列答案
相关题目
 如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是
如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是 如图ABCD是正方形,AC=10cm,求阴影部分面积.
如图ABCD是正方形,AC=10cm,求阴影部分面积.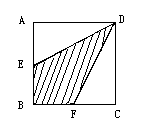
 如图ABCD是正方形,AC=10cm,求阴影部分面积.
如图ABCD是正方形,AC=10cm,求阴影部分面积.