题目内容
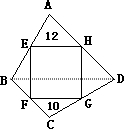
 如图,正方形EFGH的四个顶点分别是四边形ABCD各边的中点.已知△AEH、△CFG的面积分别是12平方厘米、10平方厘米,那么四边形ABCD的面积是
如图,正方形EFGH的四个顶点分别是四边形ABCD各边的中点.已知△AEH、△CFG的面积分别是12平方厘米、10平方厘米,那么四边形ABCD的面积是88
88
平方厘米.分析:连接BD.由E,F,G,H是四边形ABCD各边的中点可求得三角形相似,从而求得四边形的面积是多少.
解答:解:连接BD,如图:
因为E、H为AB、AD边中点,所以EH=
BD.
由于△AEH∽△ABD,
所以S△AEH=
S△ABD,
同理得:S△CFG=
S△CBD,
S四边形ABCD=S△ABD+S△CBD,
S四边形ABCD=12×4+10×4,
=48+40,
=88(平方厘米);
故答案为:88.

因为E、H为AB、AD边中点,所以EH=
| 1 |
| 2 |
由于△AEH∽△ABD,
所以S△AEH=
| 1 |
| 4 |
同理得:S△CFG=
| 1 |
| 4 |
S四边形ABCD=S△ABD+S△CBD,
S四边形ABCD=12×4+10×4,
=48+40,
=88(平方厘米);
故答案为:88.
点评:本题考查了三角形中位线的性质及相似多边形的性质求解.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为
如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为 [化整为零].如图,正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN(这里的内接指正方形的四个顶点全部在三角形的边上).已知正方形ABCD的面积是72平方厘米,那么正方形EFGH的面积是多少平方厘米?
[化整为零].如图,正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN(这里的内接指正方形的四个顶点全部在三角形的边上).已知正方形ABCD的面积是72平方厘米,那么正方形EFGH的面积是多少平方厘米?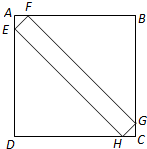 如图,正方形ABCD中,等腰直角三角形AEF的面积是1,长方形EFGH的面积是10,那么,正方形ABCD的面积是
如图,正方形ABCD中,等腰直角三角形AEF的面积是1,长方形EFGH的面积是10,那么,正方形ABCD的面积是 如图,正方形EFGH的四个顶点分别是四边形ABCD各边的中点.已知△AEH、△CFG的面积分别是12平方厘米、10平方厘米,那么四边形ABCD的面积是________平方厘米.
如图,正方形EFGH的四个顶点分别是四边形ABCD各边的中点.已知△AEH、△CFG的面积分别是12平方厘米、10平方厘米,那么四边形ABCD的面积是________平方厘米.