题目内容
如图所示，DE=4厘米，正方形ABCD的面积=56平方厘米，求BF？
解：因为DC∥AF，所以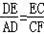
；
同理，BC∥AE，得出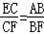
，
所以可得：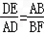
，
利用比例的基本性质得出：AD×AB=DE×BF，
AD、AB是正方形的边长，
所以AD×AB=56平方厘米，DE=4厘米，
把数据代入上式可得：56=4×BF，所以BF=14厘米；
答：BF的长是14厘米。
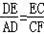；同理，BC∥AE，得出
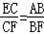，所以可得：
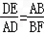，利用比例的基本性质得出：AD×AB=DE×BF，
AD、AB是正方形的边长，
所以AD×AB=56平方厘米，DE=4厘米，
把数据代入上式可得：56=4×BF，所以BF=14厘米；
答：BF的长是14厘米。
练习册系列答案
阅读快车系列答案
相关题目
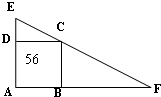如图所示，DE=4厘米，正方形ABCD的面积=56平方厘米，求BF？
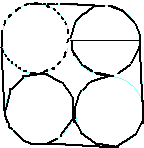小明的爸爸到商店买了4瓶啤酒，售货员将4瓶啤酒捆扎在一起，如图所示，捆4圈至少用绳子
如图所示，把4个边长是5厘米的小正方形拼成一个大正方形，这个大正方形的周长是
如图所示，DE=4厘米，正方形ABCD的面积=56平方厘米，求BF？