题目内容
 如图所示,DE=4厘米,正方形ABCD的面积=56平方厘米,求BF?
如图所示,DE=4厘米,正方形ABCD的面积=56平方厘米,求BF?
解:因为DC∥AF,所以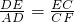 ;
;
同理,BC∥AE,得出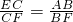 ,
,
所以可得: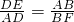 ,利用比例的基本性质得出:AD×AB=DE×BF,
,利用比例的基本性质得出:AD×AB=DE×BF,
AD、AB是正方形的边长,所以AD×AB=56平方厘米,DE=4厘米,把数据代入上式可得:
56=4×BF,
所以BF=14厘米;
答:BF的长是14厘米.
分析:此题可以利用平行线分线段成比例的性质进行解答:因为DC∥AF,所以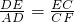 ;同理,得出
;同理,得出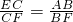 ,等量代换可得:
,等量代换可得: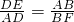 ,利用比例的基本性质得出:AD×AB=DE×BF,由此代入数据即可解答.
,利用比例的基本性质得出:AD×AB=DE×BF,由此代入数据即可解答.
点评:此题考查了平行线分线段成比例的性质以及比例的基本性质的灵活应用.
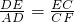 ;
;同理,BC∥AE,得出
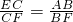 ,
,所以可得:
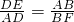 ,利用比例的基本性质得出:AD×AB=DE×BF,
,利用比例的基本性质得出:AD×AB=DE×BF,AD、AB是正方形的边长,所以AD×AB=56平方厘米,DE=4厘米,把数据代入上式可得:
56=4×BF,
所以BF=14厘米;
答:BF的长是14厘米.
分析:此题可以利用平行线分线段成比例的性质进行解答:因为DC∥AF,所以
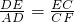 ;同理,得出
;同理,得出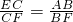 ,等量代换可得:
,等量代换可得: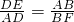 ,利用比例的基本性质得出:AD×AB=DE×BF,由此代入数据即可解答.
,利用比例的基本性质得出:AD×AB=DE×BF,由此代入数据即可解答.点评:此题考查了平行线分线段成比例的性质以及比例的基本性质的灵活应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
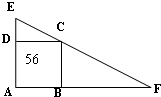 如图所示,DE=4厘米,正方形ABCD的面积=56平方厘米,求BF?
如图所示,DE=4厘米,正方形ABCD的面积=56平方厘米,求BF?