题目内容
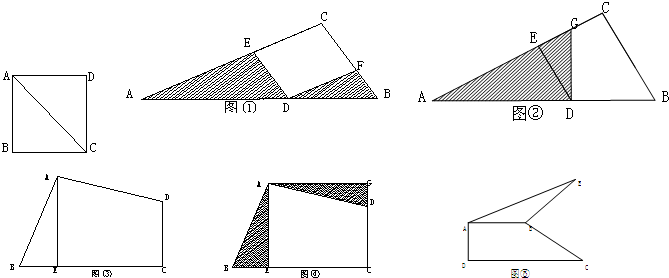
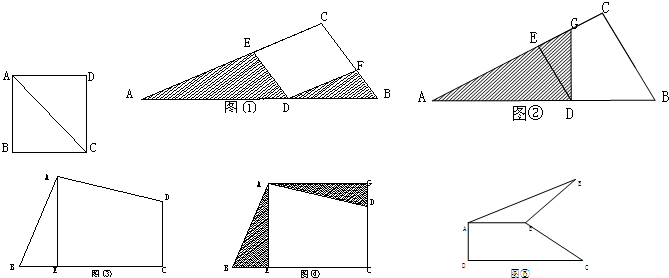
如图，在一个四边形ABCD中，AC、BD相交于点O．作三角形DBC的高DE，连接AE．若三角形ABO的面积与三角形DCO的面积相等，且DC=17厘米，DE=15厘米，则阴影部分的面积为多少平方厘米？
解：因为CE2=172-152，
=289-225，
=64，
则CE=8厘米，
所以阴影部分的面积是：8×15÷2=60（平方厘米），
答：阴影部分的面积是60平方厘米．
分析：因为三角形ABO和三角形COD面积相等，所以三角形ABC和三角形DCB面积也相等，由于两个三角形共用底边BC，所以两个三角形BC边上的高相等，于是AD与BC平行，所以三角形ACE中，CE边上的高为15厘米，又在直角三角形CDE中，于是可以求出CE的长度，再据三角形的面积公式即可求解．
点评：解答此题的关键是明白：三角形CDE是直角三角形，阴影部分和三角形CDE等底等高，则二者的面积相等．
=289-225，
=64，
则CE=8厘米，
所以阴影部分的面积是：8×15÷2=60（平方厘米），
答：阴影部分的面积是60平方厘米．
分析：因为三角形ABO和三角形COD面积相等，所以三角形ABC和三角形DCB面积也相等，由于两个三角形共用底边BC，所以两个三角形BC边上的高相等，于是AD与BC平行，所以三角形ACE中，CE边上的高为15厘米，又在直角三角形CDE中，于是可以求出CE的长度，再据三角形的面积公式即可求解．
点评：解答此题的关键是明白：三角形CDE是直角三角形，阴影部分和三角形CDE等底等高，则二者的面积相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2004?滨湖区）一个长方形，长是宽的2倍（如图）．请你把它划分成三块，使这三块能分别拼成以下各种图形：A、直角三角形；B、等腰梯形；C、平行四边形；D、正方形．
（2010?保靖县）如图，把平行四边形沿高剪开，在把三角形向右平移（ ）cm，可以得到一个与原图形面积相等的长方形．
（1）在平面内两条互相垂直而且相交于原点o的数轴，这样就建立了一个平面直角坐标系（如图）．平面内每任意一点位置都可以用一对数来表示，如A点所在位置是（2，4），
