题目内容
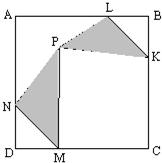 ABCD是边长为12的正方形(如图),P是内部任意一点,BL=DM=4,BK=DN=5,那么阴影部分的面积是
ABCD是边长为12的正方形(如图),P是内部任意一点,BL=DM=4,BK=DN=5,那么阴影部分的面积是分析:如下图所示,连接AP,PC,则阴影部分的面积就等于正方形ABCD的面积减去图中空白部分6个三角形的面积.由此可设△ANP的底边AN上的高为x,则△CKP的底边CK上的高即为(12-x),设△ALP的底边AL上的高为y,则△MCP的底边MC上的高即为(12-y),由三角形的面积公式即可表示出这4个三角形的面积,另外也可求得△BKL和△NDM的面积,再利用正方形的面积公式求出正方形ABCD的面积,最后用正方形ABCD的面积减去6个三角形的面积即可.
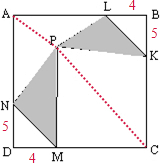

解答:解:如图,连接AP,PC,设△ANP的底边AN上的高为x,则△CKP的底边CK上的高即为(12-x);设△ALP的底边AL上的高为y,则△MCP的底边MC上的高即为(12-y),
所以S△ANP=
(12-5)x=3.5x,
S△ALP=
(12-4)y=4y,
S△MCP=
(12-4)(12-y)=4(12-y)=48-4y,
S△CKP=
(12-5)(12-x)=3.5(12-x)=42-3.5x,
S△BKL=
×4×5=10,
S△NDM=
×4×5=10,
S正方形ABCD=12×12=144,
所以阴影部分的面积是:144-3.5x-4y-(48-4y)-(42-3.5x)-10-10
=144-3.5x-4y-48+4y-42+3.5x-10-10
=144-48-42-10-10
=34;
答:阴影部分的面积是34.
故答案为:34.
所以S△ANP=
| 1 |
| 2 |
S△ALP=
| 1 |
| 2 |
S△MCP=
| 1 |
| 2 |
S△CKP=
| 1 |
| 2 |
S△BKL=
| 1 |
| 2 |
S△NDM=
| 1 |
| 2 |
S正方形ABCD=12×12=144,
所以阴影部分的面积是:144-3.5x-4y-(48-4y)-(42-3.5x)-10-10
=144-3.5x-4y-48+4y-42+3.5x-10-10
=144-48-42-10-10
=34;
答:阴影部分的面积是34.
故答案为:34.
点评:本题解题的关键是能作出辅助线,明确阴影部分的面积就等于正方形ABCD的面积减去图中空白部分6个三角形的面积.而且设出三角形的高表示出各个三角形的面积也很重要.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是
如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是 下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB、BC、CD、DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数
下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB、BC、CD、DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数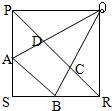 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是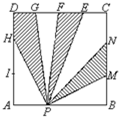 如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是________.
如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是________.