题目内容
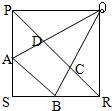 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是25.6
25.6
平方厘米.分析:用正方形面积减去△ABS、△PQA、△RQB的面积就是△ABQ的面积,然后根据BR:RQ=8:12=2:3,得出BC:QC=2:3,最后得出QC:QB=3:5,从而知道△QDC:、△QAB=9:25,又因为△QAB已知,代入数据求解即可.
解答:解:正方形PQRS=12×12=144(平方厘米),
△ABS=4×4÷2=8(平方厘米),
△PQA=△RQB=8×12÷2=48(平方厘米),
△ABQ=144-8-48-48=40(平方厘米),
C为PR上一点,故C到BR=C到QR,
故BR:RQ=8:12=2:3,
所以BC:QC=2:3,
QC:QB=3:5,
△QDC:△QAB=9:25,
梯形ABCD=40×
,
=40×
,
=25.6(平方厘米),
故答案为:25.6.
△ABS=4×4÷2=8(平方厘米),
△PQA=△RQB=8×12÷2=48(平方厘米),
△ABQ=144-8-48-48=40(平方厘米),
C为PR上一点,故C到BR=C到QR,
故BR:RQ=8:12=2:3,
所以BC:QC=2:3,
QC:QB=3:5,
△QDC:△QAB=9:25,
梯形ABCD=40×
| 25-9 |
| 25 |
=40×
| 16 |
| 25 |
=25.6(平方厘米),
故答案为:25.6.
点评:此题考查了求组合图形的面积,在计算过程中关键是求出△QDC和△QAB的比是多少.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍? 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.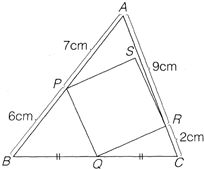 如图,正方形PQRS有三个顶点分别在三角形ABC的三条边上,BQ=QC,请求出正方形PQRS的面积.
如图,正方形PQRS有三个顶点分别在三角形ABC的三条边上,BQ=QC,请求出正方形PQRS的面积. 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是________平方厘米.
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是________平方厘米.