题目内容
18.图中阴影部分的面积是48平方厘米,A、B是两边的中点.你能求出图中平行四边形的面积吗?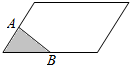
分析 如图,连结DC、DB,因为A、B是两边的中点,所以推出△ABE与△EBD以及△ABD与△DEC之间的面积关系,从而得出△ABE的面积等于$\frac{1}{4}$△DEC的面积,又因为△DEC的面积等于$\frac{1}{2}$平行四边形的面积,进而得解.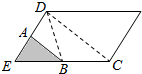
解答 解:连结DC、DB,因为A、B是△EBD边的中点,
所以S△ABE=$\frac{1}{2}$S△EBD,
所以S△EBD=2×48=96(平方厘米),
又因为B是EC的中点,
所以S△DEC=2S△EBD=2×96=192(平方厘米);
又因为S△DEC=$\frac{1}{2}$S平行四边形,
所以平行四边形的面积为192×2=384(平方厘米)
答:图中平行四边形的面积为384平方厘米.
点评 此题解答的关键在于运用三角形面积与底的正比关系求出各三角形之间的面积关系,进而得解.

练习册系列答案
相关题目
13.有两杯糖水,第一杯糖和水的重量比是1:20,第二杯糖和水的重量比是1:25.比较两杯糖水( )
| A. | 第一杯甜些 | B. | 第二杯甜些 | C. | 两杯一样甜 | D. | 无法比较 |