题目内容
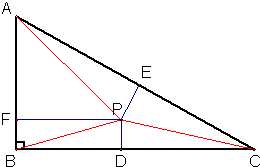
如图所示,直角三角形ABC中,AB=5,BC=12,CA=13,PD、PE、PF分别垂直于边BC、CA、AB,其中D、E、F是垂足,已知PD=1,PE=2,则PF=
4.4
4.4

分析:先连接PA、PB、PC,根据直角三角形ABC中,底AB=5,高BC=12,可求出三角形ABC的面积;根据三角形APC中底AC=13,高PE=2,可求出三角形APC的面积;根据三角形BPC中底BC=12,高PD=1,可求出三角形BPC的面积;再根据三角形ABC的面积-(三角形APC的面积+三角形BPC的面积)=三角形APB的面积,进而根据三角形APB的面积和底求得高PF的长度即可.


解答:解:连接PA、PB、PC,由题意得:
三角形ABC的面积:
×5×12=30,
三角形APC的面积:
×13×2=13,
三角形BPC的面积:
×12×1=6,
所以三角形APB的面积:30-(13+6)=30-19=11,
所以三角形APB的高:11÷
÷5=22÷5=4.4;
故答案为:4.4.
三角形ABC的面积:
| 1 |
| 2 |
三角形APC的面积:
| 1 |
| 2 |
三角形BPC的面积:
| 1 |
| 2 |
所以三角形APB的面积:30-(13+6)=30-19=11,
所以三角形APB的高:11÷
| 1 |
| 2 |
故答案为:4.4.
点评:解决此题关键是先求得三角形ABC、APC、BPC和APB的面积,再根据它们之间的关系,求得PF的长度即可.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图所示:直角三角形的三边长分别为6cm、8cm、10cm,则边长为10cm的边上的高为
如图所示:直角三角形的三边长分别为6cm、8cm、10cm,则边长为10cm的边上的高为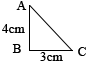 (2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个
(2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个 请你在卡纸上画4个如图所示的直角三角形(单位:厘米)将它们剪下并拼成一个中间有一个小正方形空洞的大正方形.
请你在卡纸上画4个如图所示的直角三角形(单位:厘米)将它们剪下并拼成一个中间有一个小正方形空洞的大正方形.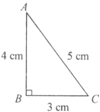 把如图所示的直角三角形ABC沿着AB轴旋转一周,形成
把如图所示的直角三角形ABC沿着AB轴旋转一周,形成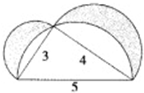 如图所示,直角三角形的直角边与斜边的长分别是3,4,5,以三边为直径分别作圆,则阴影部分的面积是
如图所示,直角三角形的直角边与斜边的长分别是3,4,5,以三边为直径分别作圆,则阴影部分的面积是