题目内容
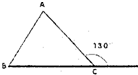 如图是一个等腰三角形,AC=BC,则∠ABC=________度.
如图是一个等腰三角形,AC=BC,则∠ABC=________度.
65
分析:先根据邻补角的定义求出∠ACB的度数,再根据三角形的内角和定理和等腰三角形的性质即可求得∠ABC的度数.
解答:∠ACB=180°-130°=50°,
∠ABC=(180°-50°)÷2=65°.
故答案为:65.
点评:考查了邻补角的定义、三角形的内角和是180°以及等腰三角形的两底角相等的性质,注意综合运用.
分析:先根据邻补角的定义求出∠ACB的度数,再根据三角形的内角和定理和等腰三角形的性质即可求得∠ABC的度数.
解答:∠ACB=180°-130°=50°,
∠ABC=(180°-50°)÷2=65°.
故答案为:65.
点评:考查了邻补角的定义、三角形的内角和是180°以及等腰三角形的两底角相等的性质,注意综合运用.

练习册系列答案
相关题目
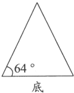 如图是一个等腰三角形.
如图是一个等腰三角形.  (2004?陆良县)如图是一个等腰三角形.
(2004?陆良县)如图是一个等腰三角形. (2011?河池)如图是一个等腰三角形,面积是5平方分米.
(2011?河池)如图是一个等腰三角形,面积是5平方分米.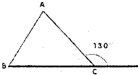 如图是一个等腰三角形,AC=BC,则∠ABC=
如图是一个等腰三角形,AC=BC,则∠ABC=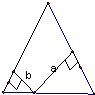 如图是一个等腰三角形,它的腰长是20cm,面积是144cm2.在底边上任取一点,向两腰作垂线得a和b,a+b=
如图是一个等腰三角形,它的腰长是20cm,面积是144cm2.在底边上任取一点,向两腰作垂线得a和b,a+b=