题目内容
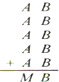如图所示，5个相同的两位数. |
| AB |
. |
| MB |
. |
| AB |
10或15
10或15
．分析：根据整数加法竖式计算的方法进行推算即可．
解答：解：根据题意，由加法竖式可得：
个位上，5×B的末尾还是B，由5×0=0，5×5=25可得：B=0或B=5；
假设B=0，那么十位上，5×A=M，M要小于10，只有当A=1时，5×1=5，符合；
所以，A=1，B=0；
由以上推算可得：
假设B=5时，5×5=25，向十位进2；
十位上，5×A+2=M，M要小于10，只有当A=1时，5×1+2=7，符合；
所以，A=1，B=5；
由以上推算可得：
因此两位数
是：10或15．
故答案为：10或15．
个位上，5×B的末尾还是B，由5×0=0，5×5=25可得：B=0或B=5；
假设B=0，那么十位上，5×A=M，M要小于10，只有当A=1时，5×1=5，符合；
所以，A=1，B=0；
由以上推算可得：
假设B=5时，5×5=25，向十位进2；
十位上，5×A+2=M，M要小于10，只有当A=1时，5×1+2=7，符合；
所以，A=1，B=5；
由以上推算可得：
因此两位数
. |
| AB |
故答案为：10或15．
点评：推算过程中，本题的关键是末尾数字相同，然后再进一步解答即可．
练习册系列答案
相关题目
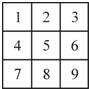用红、黄、蓝三种颜色之一去涂图中标号为1，2，…，9的9个小正方形（如图所示），使得任意相邻（有公共边的）小正方形所涂颜色都不相同，若标号为“1、5、9”的小正方形涂相同的颜色，则符合条件的所有涂法共有
有三个圆心相同的半圆，它们的直径分别为1、3、5，用线段将其分割成9块，如图所示，如果每块中的字母代表着这一块面积，并且相同字母表示相同的面积，那么A：B=
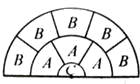有三个圆心相同的半圆，它们的直径分别为1、3、5，用线段将其分割成9块，如图所示，如果每块中的字母代表着这一块面积，并且相同字母表示相同的面积，那么A：B=________．