题目内容
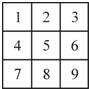 用红、黄、蓝三种颜色之一去涂图中标号为1,2,…,9的9个小正方形(如图所示),使得任意相邻(有公共边的)小正方形所涂颜色都不相同,若标号为“1、5、9”的小正方形涂相同的颜色,则符合条件的所有涂法共有
用红、黄、蓝三种颜色之一去涂图中标号为1,2,…,9的9个小正方形(如图所示),使得任意相邻(有公共边的)小正方形所涂颜色都不相同,若标号为“1、5、9”的小正方形涂相同的颜色,则符合条件的所有涂法共有A
A
.A、108种; B、60种; C、48种; D、36种.
分析:当1,5,9,为其中一种颜色时,2,6共有4种可能,其中2种2,6是涂相同颜色,各有2种可能共6种可能.4,8及7,与2,6及3,一样有6种可能并且与2,6,3,颜色无关,当1,5,9换其他的颜色时也是相同的情况,相乘得到结果.
解答:解:首先看图形中的1,5,9,有3种可能,
当1,5,9,为其中一种颜色时,
2,6共有4种可能,其中2种2,6是涂相同颜色,各有2种可能共6种可能.
4,8及7,与2,6及3,一样有6种可能并且与2,6,3,颜色无关.
当1,5,9换其他的颜色时也是相同的情况,
符合条件的所有涂法共有3×6×6=108种;
故选:A.
当1,5,9,为其中一种颜色时,
2,6共有4种可能,其中2种2,6是涂相同颜色,各有2种可能共6种可能.
4,8及7,与2,6及3,一样有6种可能并且与2,6,3,颜色无关.
当1,5,9换其他的颜色时也是相同的情况,
符合条件的所有涂法共有3×6×6=108种;
故选:A.
点评:本题考查分别计数原理,考查分类原理,是一个限制元素比较多的题目,解题时注意分类,做到不重不漏.

练习册系列答案
相关题目
 用红、黄、蓝三种颜色给下面的两个长方格子涂颜色:一个格子涂一种颜色,两个格子要涂上不同的颜色,一共有
用红、黄、蓝三种颜色给下面的两个长方格子涂颜色:一个格子涂一种颜色,两个格子要涂上不同的颜色,一共有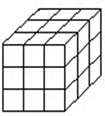 有一个3×3×3的正方体,要求用红、黄、蓝三种颜色去染这些小正方形,并且有公共边的正方形要染不同的颜色.那么,用红色染的正方形最多有多少个?
有一个3×3×3的正方体,要求用红、黄、蓝三种颜色去染这些小正方形,并且有公共边的正方形要染不同的颜色.那么,用红色染的正方形最多有多少个?