题目内容
三个同心圆的半径之比是3:4:5,如果大圆的面积是100平方厘米,那么中圆与小圆构成的圆环面积是多少平方厘米?
解:根据题干分析可得:圆的面积与半径的平方成正比例,三个同心圆的半径之比是3:4:5,
则它们的面积之比就是32:42:52=9:16:25,
又因为最大的圆的面积是100,
所以中圆的面积是:100×16÷25=64(平方厘米),
则小圆的面积是100×9÷25=36(平方厘米),
64-36=28(平方厘米);
答:中圆与小圆构成的圆环面积是28平方厘米.
分析:根据圆的面积公式可知:圆的面积与半径的平方成正比例,三个同心圆的半径之比是3:4:5,则它们的面积之比就是32:42:52=9:16:25,又因为最大的圆的面积是100,据此即可分别求出另外两个圆的面积,再相减即可求出它们组成的圆环的面积.
点评:此题主要考查圆的面积与半径的平方成正比例的性质的灵活应用以及比例的基本性质、圆环的面积公式的计算应用.
则它们的面积之比就是32:42:52=9:16:25,
又因为最大的圆的面积是100,
所以中圆的面积是:100×16÷25=64(平方厘米),
则小圆的面积是100×9÷25=36(平方厘米),
64-36=28(平方厘米);
答:中圆与小圆构成的圆环面积是28平方厘米.
分析:根据圆的面积公式可知:圆的面积与半径的平方成正比例,三个同心圆的半径之比是3:4:5,则它们的面积之比就是32:42:52=9:16:25,又因为最大的圆的面积是100,据此即可分别求出另外两个圆的面积,再相减即可求出它们组成的圆环的面积.
点评:此题主要考查圆的面积与半径的平方成正比例的性质的灵活应用以及比例的基本性质、圆环的面积公式的计算应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是
如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是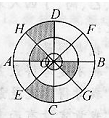 如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是________.
如图,三个同心圆的半径分别是1厘米,3厘米,5厘米,AB,CD,EF,GH八等分这个圆,且都过圆心O.图中阴影部分的面积与非阴影部分的面积之比是________.