题目内容
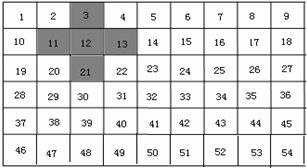
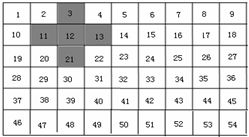 把1~54这54个数从小到大排成一行(如表),
把1~54这54个数从小到大排成一行(如表),(1)算一算,上表中被阴影覆盖的5个数和是多少?这5个数的和与中间的数有什么关系?
(2)如果框出的5个数的和是165,请你框出这5个数.
(3)像这样框出5个数,一共可以得到多少个不同的和?
分析:(1)将5个数相加即可;即3+11+12+13+21=60;5个数的和是60,是中间数12的5倍;
(2)因为这5个数的和是中间的数的5倍,所以中间数是165÷5=33,则框出的5个数为:24、32、33、34、42;
(3)最上边一行能框的数从2开始,到8结束,有9-2=7个;竖着能框出的数有6-2=4行,总共有:7×4=28(个).
据此解答即可.
(2)因为这5个数的和是中间的数的5倍,所以中间数是165÷5=33,则框出的5个数为:24、32、33、34、42;
(3)最上边一行能框的数从2开始,到8结束,有9-2=7个;竖着能框出的数有6-2=4行,总共有:7×4=28(个).
据此解答即可.
解答:解:由分析得:
(1)上表中被阴影覆盖的5个数和是:3+11+12+13+21=60;
60÷12=5,所以这5个数的和是中间的数的5倍;
(2)因为这5个数的和是中间的数的5倍,所以中间数是165÷5=33,则框出的5个数为:24、32、33、34、42;
5个数如图所示: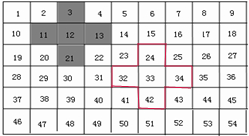 ;
;
(3)总共可以框出:(9-2)×(6-2)=28(个).
答:一共可以框出28个不同的和.
(1)上表中被阴影覆盖的5个数和是:3+11+12+13+21=60;
60÷12=5,所以这5个数的和是中间的数的5倍;
(2)因为这5个数的和是中间的数的5倍,所以中间数是165÷5=33,则框出的5个数为:24、32、33、34、42;
5个数如图所示:
 ;
;(3)总共可以框出:(9-2)×(6-2)=28(个).
答:一共可以框出28个不同的和.
点评:解决本题的关键是找到规律,再结合问题解答.

练习册系列答案
相关题目
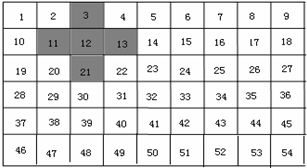
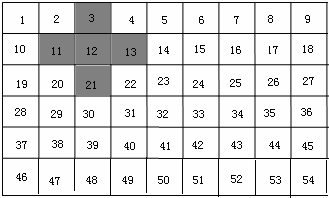
 把1~54这54个数从小到大排成一行(如表),
把1~54这54个数从小到大排成一行(如表),