题目内容
 如图,已知长方形ADEF的面积24,三角形ADB的面积是4,三角形ACF的面积是6,那么三角形ABC的面积是
如图,已知长方形ADEF的面积24,三角形ADB的面积是4,三角形ACF的面积是6,那么三角形ABC的面积是10
10
.分析:根据长方形ADEF的面积24,可设AD=x,进而用含x的式子表示出AF=
;根据三角形ADB的面积是4,可求出BD的长度,进而求出BE的长度;根据三角形ACF的面积是6,可求出FC的长度,进而求出CE的长度;知道了BE和CE的长度,即可求出△BEC的面积,再用S矩形ADEF减去S△ADB减去S△ACF减去S△BCE,即得S△ABC.
| 24 |
| x |
解答:解:∵ADEF是矩形,
∴AD=EF,AF=DE,
∠D=∠E=∠F=90°,
设AD=EF=x,
∴AF=DE=
;
∵在Rt△ADB中:S△ADB=
×x×BD=4,
∴BD=
,
∴BE=DE-BD=
-
=
;
∵在Rt△ACF中:S△ACF=
×
×CF=6,
∴CF=
,
∴CE=EF-CF=X-
=
;
∴在Rt△BCE中:S△BCE=
×
×
=4,
∴S△ABC=S矩形ADEF-S△ADB-S△ACF-S△BCE=24-4-6-4=10;
故答案为:10.
∴AD=EF,AF=DE,
∠D=∠E=∠F=90°,
设AD=EF=x,
∴AF=DE=
| 24 |
| x |
∵在Rt△ADB中:S△ADB=
| 1 |
| 2 |
∴BD=
| 8 |
| x |
∴BE=DE-BD=
| 24 |
| x |
| 8 |
| x |
| 16 |
| x |
∵在Rt△ACF中:S△ACF=
| 1 |
| 2 |
| 24 |
| x |
∴CF=
| x |
| 2 |
∴CE=EF-CF=X-
| x |
| 2 |
| x |
| 2 |
∴在Rt△BCE中:S△BCE=
| 1 |
| 2 |
| 16 |
| x |
| x |
| 2 |
∴S△ABC=S矩形ADEF-S△ADB-S△ACF-S△BCE=24-4-6-4=10;
故答案为:10.
点评:求出△BEC的面积是解决本题的关键,据此先求出BE和EC的长度,进而用S矩形ADEF减去S△ADB减去S△ACF减去S△BCE,即得S△ABC.

练习册系列答案
相关题目
 如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积.
如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积. 已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米?
已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米? 如图,已知ABCD和AEFG是两个能完全重合的长方形,且AD边恰好在AE边上,如果BG=18厘米,DE=9厘米,求长方形ABCD的面积.
如图,已知ABCD和AEFG是两个能完全重合的长方形,且AD边恰好在AE边上,如果BG=18厘米,DE=9厘米,求长方形ABCD的面积.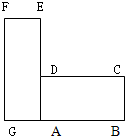 如图,已知ABCD和AEFG是两个能完全重合的长方形,且AD边恰好在AE边上,如果BG=18厘米,DE=9厘米,求长方形ABCD的面积.
如图,已知ABCD和AEFG是两个能完全重合的长方形,且AD边恰好在AE边上,如果BG=18厘米,DE=9厘米,求长方形ABCD的面积. 如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积.
如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积.