题目内容
有一个圆柱和一个圆锥,圆柱的底面积是圆锥底面积的
,圆锥的高是圆柱高的2倍.这个圆柱和圆锥的体积之比是多少?
| 2 | 5 |
分析:要求这个圆柱和圆锥的体积比是多少,先要分别求出圆柱和圆锥的体积;根据“圆柱的体积=底面积×高”,求出圆柱的体积;然后根据“圆锥的体积=
sh”,求出圆锥的体积,最后进行比即可.
| 1 |
| 3 |
解答:解:假设圆柱的底面积为s,高为h,
则圆锥底面积为:s÷
=
s,
圆柱的体积:v=sh,
圆锥的体积:
×
s×(2h)=
sh,
圆柱和圆锥体积比为:sh:
sh=3:5;
答:圆柱和圆锥的体积比为3:5.
则圆锥底面积为:s÷
| 2 |
| 5 |
| 5 |
| 2 |
圆柱的体积:v=sh,
圆锥的体积:
| 1 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
圆柱和圆锥体积比为:sh:
| 5 |
| 3 |
答:圆柱和圆锥的体积比为3:5.
点评:解答此题要先分别求出圆柱和圆锥的体积,再求比.

练习册系列答案
相关题目
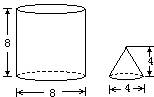 这里有一个圆柱和一个圆锥(如图),它们的高和底面直径都标在图上,单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?
这里有一个圆柱和一个圆锥(如图),它们的高和底面直径都标在图上,单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?