题目内容
如图，在矩形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示．试求图中阴影部分的总面积．
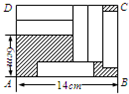
分析：设长方形的长和宽为未数，根据图示可得到关于xy的两个方程，可求得解，从而可得到大长方形的面积，再根据阴影部分的面积=大长方形的面积-6个小长方形的面积求解即可．
解答：解：设小长方形的长为x，宽为y，如图可知，
x+3y=14，①
x+y-2y=6，即x-y=6，②
①-②得4y=8，
y=2，
代入②得x=8，
因此，大矩形ABCD的宽AD=6+2y=6+2×2=10．
矩形ABCD面积=14×10=140（平方厘米），
阴影部分总面积=140-6×2×8=44（平方厘米）．
x+3y=14，①
x+y-2y=6，即x-y=6，②
①-②得4y=8，
y=2，
代入②得x=8，
因此，大矩形ABCD的宽AD=6+2y=6+2×2=10．
矩形ABCD面积=14×10=140（平方厘米），
阴影部分总面积=140-6×2×8=44（平方厘米）．
点评：本题考查了二元一次方程的应用，以及学生对图表的阅读理解能力．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．
练习册系列答案
名校课堂系列答案
相关题目
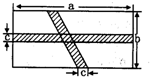如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，其中a=10，b=5，c=1，计算图中空白部分的面积，其面积是（ ）
如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为
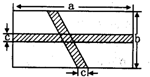如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，其中a=10，b=5，c=1，计算图中空白部分的面积，其面积是