题目内容
如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为| 3 |
| 3 |
分析：首先连接CC'，可以得到CC′是角EC'D的平分线，所以CB′=CD 又AB′=AB，所以B′是对角线中点，AC=2AB，所以∠ACB=30°，即可得出答案．
解答：解：连接CC′，
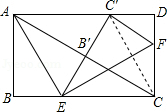
因为将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处所以EC=EC′，
所以∠EC′C=∠ECC′；
因为∠DC′C=∠ECC′，
所以∠EC′C=∠DC′C，
所以得到CC′是∠EC'D的平分线；
因为∠CB′C′=∠D=90°，
所以CB′=CD；
又因为AB′=AB，
所以B′是对角线AC中点，即AC=2AB，
所以∠ACB=30°，
所以cot∠ACB=cot30°=
=
，
BC：AB的值为
：
故答案为：
．
因为将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处所以EC=EC′，
所以∠EC′C=∠ECC′；
因为∠DC′C=∠ECC′，
所以∠EC′C=∠DC′C，
所以得到CC′是∠EC'D的平分线；
因为∠CB′C′=∠D=90°，
所以CB′=CD；
又因为AB′=AB，
所以B′是对角线AC中点，即AC=2AB，
所以∠ACB=30°，
所以cot∠ACB=cot30°=
| BC |
| AB |
| 3 |
BC：AB的值为
| 3 |
故答案为：
| 3 |
点评：认真观察图形，通过作辅助线，运用初中数学知识三角函数，进行解答．
练习册系列答案
相关题目
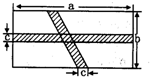如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，其中a=10，b=5，c=1，计算图中空白部分的面积，其面积是（ ）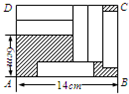
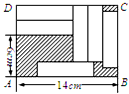
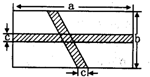如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，其中a=10，b=5，c=1，计算图中空白部分的面积，其面积是