题目内容
如果一个长方形的长、宽都是整数(长与宽不相等).且周长与面积的数值相等,那么这个长方形的面积的数值等于________.
16或18
分析:设长方形的长、宽分别为a、b,根据长方形周长与面积的数值相等可得出ab=2(a+b),由a b为整数,
即可求出a、b的对应值,进而可得出长方形的面积.
解答:设长方形的长、宽分别为a、b,
因为它的周长与面积的数值相等,
所以ab=2(a+b),即ab-2a-2b=0,a(b-2)=2b,
所以a=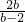 ,
,
因为a b为整数,
所以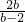 为整数,
为整数,
因为周长为整数,
所以2b+2为整数,
所以2b+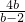 =2b+
=2b+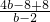 =2b+
=2b+ =2b+4+
=2b+4+ 为整数,
为整数,
所以b为3或4或6,
所以a为6或4或3,
所以这个长方形面积的数值是16或18.
故答案为:16或18.
点评:本题考查的是不定方程的应用,解答此类题目是一定要注意a b均为整数这一关键条件.
分析:设长方形的长、宽分别为a、b,根据长方形周长与面积的数值相等可得出ab=2(a+b),由a b为整数,
即可求出a、b的对应值,进而可得出长方形的面积.
解答:设长方形的长、宽分别为a、b,
因为它的周长与面积的数值相等,
所以ab=2(a+b),即ab-2a-2b=0,a(b-2)=2b,
所以a=
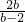 ,
,因为a b为整数,
所以
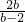 为整数,
为整数,因为周长为整数,
所以2b+2为整数,
所以2b+
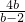 =2b+
=2b+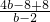 =2b+
=2b+ =2b+4+
=2b+4+ 为整数,
为整数,所以b为3或4或6,
所以a为6或4或3,
所以这个长方形面积的数值是16或18.
故答案为:16或18.
点评:本题考查的是不定方程的应用,解答此类题目是一定要注意a b均为整数这一关键条件.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目