题目内容
已知ab=1，试求
+
的值．
| a |
| 1+a |
| b |
| 1+b |
考点：含字母式子的求值
专题：用字母表示数
分析：先把
+
通分成同分母分数，进而把ab=1代入式子即可得解．
| a |
| 1+a |
| b |
| 1+b |
解答：
解：
+
=
+
=
=
把ab=1代入=
中
原式=
=1．
| a |
| 1+a |
| b |
| 1+b |
=
| a(1+b) |
| (1+a)(1+b) |
| b(1+a) |
| (1+a)(1+b) |
=
| a+ab+b+ab |
| 1+b+a+ab |
=
| a+b+2ab |
| a+b+ab+1 |
把ab=1代入=
| a+b+2ab |
| a+b+ab+1 |
原式=
| a+b+2 |
| a+b+2 |
点评：解决此题关键是把原来含字母的式子进行通分计算，再把ab=1代入计算得解．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
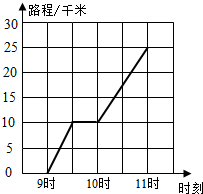填一填．如图是明华骑自行车行程情况图，看图填空．