题目内容
【题目】如图,三角形ABC是等腰直角三角形,斜边AB=12厘米,MN是BC的![]() ,AP是AC的
,AP是AC的![]() ,求三角形PMN的面积.
,求三角形PMN的面积.

【答案】9平方厘米
【解析】
试题分析:如图所示,作三角形ABC斜边上的高CE,又因等腰直角三角形斜边上的高等于斜边的一半,则CE=![]() AB=6厘米,于是可以求出三角形ABC的面积,又因AP=
AB=6厘米,于是可以求出三角形ABC的面积,又因AP=![]() AC,则PC=
AC,则PC=![]() AC,所以三角形PCB的面积等于三角形ABC的面积的
AC,所以三角形PCB的面积等于三角形ABC的面积的![]() ,又因MN=
,又因MN=![]() BC,则三角形PMN的面积等于三角形PCD的面积的
BC,则三角形PMN的面积等于三角形PCD的面积的![]() ,据此即可求出阴影部分的面积.
,据此即可求出阴影部分的面积.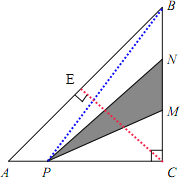
解:据分析可知:CE=![]() AB=6厘米,
AB=6厘米,
则三角形ABC的面积为:![]() =36平方厘米,
=36平方厘米,
又因AP=![]() AC,则PC=
AC,则PC=![]() AC,
AC,
所以三角形PCB的面积等于三角形ABC的面积的![]() ,即三角形PCB的面积为
,即三角形PCB的面积为![]() =27平方厘米,
=27平方厘米,
又因MN=![]() BC,则三角形PMN的面积等于三角形PCD的面积的
BC,则三角形PMN的面积等于三角形PCD的面积的![]() ,
,
即三角形PMN的面积为27×![]() =9平方厘米.
=9平方厘米.
答:三角形PMN的面积是9平方厘米.

练习册系列答案
相关题目