题目内容
观察下面按规律排成的一列数:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,…
(1)若将左起第m个数记为f(m),当f(m)=
时,求m的值和这m个数的积.
(2)在数列中,未经约分且分母为2的数记为a,它后面的一个数记为b,若存在这样的a和b,使ab=20100,求a和b.
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 1 |
| 1 |
| 5 |
| 2 |
| 4 |
| 3 |
| 3 |
| 4 |
| 2 |
| 5 |
| 1 |
| 1 |
| 6 |
(1)若将左起第m个数记为f(m),当f(m)=
| 2 |
| 2001 |
(2)在数列中,未经约分且分母为2的数记为a,它后面的一个数记为b,若存在这样的a和b,使ab=20100,求a和b.
分析:(1)从左起分别以1个数,2个数,3个数…为一组,每组的乘积为1.组内分子以1为公差递增,分母以1为公差递减.所以f(m)=
为2002组内第二项,
是第1+2+3+…+2001+1=2003002个数,m=2003003,积为1×1×1…1×
×
=
;
(2)设a为
,b=x+1即(x+1)x=2001000×2,由此即可求出a与b的值.
| 2 |
| 2001 |
| 1 |
| 2002 |
| 1 |
| 2002 |
| 2 |
| 2001 |
| 1 |
| 2003001 |
(2)设a为
| x |
| 2 |
解答:解:(1)因为从左起分别以1个数,2个数,3个数…为一组,每组的乘积为1,组内分子以1为公差递增,分母以1为公差递减.
所以f(m)=
为2002组内第二项,
是第1+2+3+…+2001+1=2003002个数,m=2003003,
积为1×1×1…1×
×
=
;
(2)设a为
,b=x+1即(x+1)x=2001000×2,
解得x1=-2002(舍),x2=2000,
b=x+1=2000+1=2001,
a=
=
;
答:(1)m的值是2003003,这m个数的积是
;(2)a是
,b是2001.
所以f(m)=
| 2 |
| 2001 |
| 1 |
| 2002 |
积为1×1×1…1×
| 1 |
| 2002 |
| 2 |
| 2001 |
| 1 |
| 2003001 |
(2)设a为
| x |
| 2 |
解得x1=-2002(舍),x2=2000,
b=x+1=2000+1=2001,
a=
| x |
| 2 |
| 2000 |
| 2 |
答:(1)m的值是2003003,这m个数的积是
| 1 |
| 2003001 |
| 2000 |
| 2 |
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,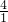 ,
, ,
, ,
,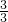 ,
, ,
,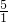 ,
, ,…
,…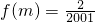 时,求m的值和这m个数的积.
时,求m的值和这m个数的积. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…
,…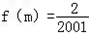 时,求m的值和这m个数的积;
时,求m的值和这m个数的积;