题目内容
5.把一个体积为30dm3的正方体木块削成最大的圆锥体后,圆锥体的体积是多少?分析 根据题意可知:把这个正方体削成最大的圆锥,圆锥的底面直径和高都等于正方体的棱长,首先求出正方体的棱长,再根据圆锥的体积的公式:v=$\frac{1}{3}sh$,把数据代入公式解答.
解答 解:设最大圆锥的底面半径为R分米,
则最大圆锥的高是2R分米,正方体木块的棱长也是2R分米,
正方体的体积是30立方分米,则有
(2R)×(2R)×(2R)=30
8R3=30
R3=$\frac{15}{4}$
最大圆锥的体积
=3.14×R2×(2R)×$\frac{1}{3}$
=$\frac{6.28}{3}×$R3
=$\frac{6.28}{3}×\frac{15}{4}$
=7.85(立方分米),
答:圆锥体的体积是7.85立方分米.
点评 此题主要考查正方体的体积公式、圆锥的特征公式的灵活运用,关键是熟记公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
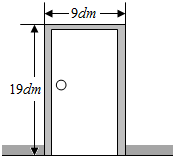 用宽为1分米、长为1米的木板条装饰门框,如图.
用宽为1分米、长为1米的木板条装饰门框,如图.