题目内容
18．有两块大小不等的正方形瓷砖，它们的边长之比是2：3，这两块瓷砖面积的比是多少？分析 可以利用代入法，正方形的面积公式是边长×边长，如果大正方形的边长是3X则面积是3X×3X=9X2，则小正方形的边长就是2X，面积就是2X×2X=4X2．然后把它们的面积作比、化简即可求解．
解答 解：设大正方形的边长是3X，则小正方形的边长是2X，
小正方形的面积：大正方形的面积=（2X×2X）：（3X×3X）
=4X2：9X2
=4：9
答：这两块瓷砖面积的比是4：9．
点评 正方形的面积的比就是边长的比的平方．而不是边长的比．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
10．
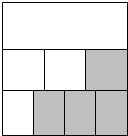把三个同样大小的长方形拼在一起，拼成一个大长方形，把第二个小长方形平均分成3份，再把第三个小长方形平均分成4份，那么阴影部分面积占大长方形面积的（ ）
把三个同样大小的长方形拼在一起，拼成一个大长方形，把第二个小长方形平均分成3份，再把第三个小长方形平均分成4份，那么阴影部分面积占大长方形面积的（ ）| A． | $\frac{7}{12}$ | B． | $\frac{13}{36}$ | C． | $\frac{1}{3}$ | D． | $\frac{5}{12}$ |
1．把一个正方体平均分成两个长方体，表面积会增加（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |