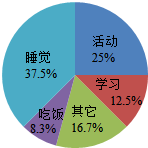
题目内容
8.(1)直角三角形中,一个锐角是25°,另一个锐角是65°.(2)一个等腰三角形其中一个角是120°,它的另外两个角都是30°.
分析 (1)根据直角三角形中的两个锐角互余即可求解;
(2)根据等腰三角形的及三角形的内角和定理可知:120°的角必是顶角,所以另外两个角分别是30°、30°.
解答 解:(1)因为直角三角形中一个锐角是25°,
所以另一个锐角是90°-25°=65°.
(2)当顶角为120°时,底角的度数为(180°-120°)÷2=30°;
当底角为120°时,两底角的度数和为:120°×2=240°>180°,因此这种情况不成立.
故答案为:65、30.
点评 (1)考查了直角三角形的两个锐角互余的性质.
(2)本题主要考查了等腰三角形的性质及三角形的内角和定理.此问题也要分类讨论,只是120°的角为底角是不成立的,要舍去,所以只有一种情况.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.直接写出得数
| 7×600= | 20×250= | 7×120= | 420×2= |
| 230×2= | 330×30= | 600×70= | 500×7= |
| 50×600= | 18×30= | 420÷60= | 800÷50= |
13.一听易拉罐可乐的净含量大约有( )毫升?
| A. | 35毫升 | B. | 3500毫升 | C. | 350毫升 |
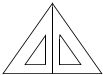 用两块同样的三角板拼成一个大三角形,(如图)如果按角分,那么拼成的三角形是锐角三角形,按边分,那么拼成的三角形是等边三角形.
用两块同样的三角板拼成一个大三角形,(如图)如果按角分,那么拼成的三角形是锐角三角形,按边分,那么拼成的三角形是等边三角形.