题目内容
应用比例的性质,判断下面哪组中的两个比可以组成比例.(能的在横线里打“√”,并把组成的比例写出来,不能的打“×”)
(1)3:1.5和4:2.5
(2)0.4:5和8:100
(3)
:
和
:
(4)2.4:
和
:5
(1)3:1.5和4:2.5
×
×
(2)0.4:5和8:100
√0.4:5=8:100
√0.4:5=8:100
(3)
| 1 |
| 5 |
| 1 |
| 10 |
| 1 |
| 3 |
| 1 |
| 10 |
×
×
(4)2.4:
| 3 |
| 5 |
| 5 |
| 6 |
×
×
.分析:根据比例的基本性质“两外项的积等于两内项的积”,分别计算求出两内项的积和两外项的积,如果等于,就说明两个比能组成比例,不等于就不能组成比例.
解答:解:(1)因为3×2.5≠1.5×4,所以3:1.5和4:2.5不能组成比例;
(2)因为0.4×100=5×8,所以0.4:5和8:100能组成比例;
组成的比例为:0.4:5=8:100;
(3)因为
×
≠
×
,所以
:
和
:
不能组成比例;
(4)因为2.4×5≠
×
,所以2.4:
和
:5不能组成比例;
故答案为:×,√0.4:5=8:100,×,×.
(2)因为0.4×100=5×8,所以0.4:5和8:100能组成比例;
组成的比例为:0.4:5=8:100;
(3)因为
| 1 |
| 5 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 10 |
| 1 |
| 3 |
| 1 |
| 10 |
(4)因为2.4×5≠
| 3 |
| 5 |
| 5 |
| 6 |
| 3 |
| 5 |
| 5 |
| 6 |
故答案为:×,√0.4:5=8:100,×,×.
点评:此题考查用比例的性质辨识两个比能否组成比例,关键是看这两个比的内项与外项的乘积,如果能组成比例,它的两内项的积等于两外项的积.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
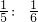 和6:5
和6:5 :45和0.2:70.
:45和0.2:70.