题目内容
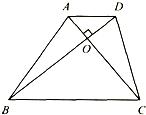
如图,梯形ABCD的对角线相互垂直.三角形AOB的面积是12,OD的长是4,求OC的长.

考点:梯形的面积
专题:几何的计算与计数专题
分析:因为三角形ABD与三角形ACD等底等高,所以这两个三角形面积相等,又因为三角形AOD是公共部分,所以三角形ABO与三角形OCD的面积相等都是12,已知道OD的长是4,然后根据三角形的面积公式即可求出OC的长.
解答:
解:12×2÷4
=24÷4
=6
答:OC的长是6.
=24÷4
=6
答:OC的长是6.
点评:本题主要考查了等底等高的三角形的面积相等这一知识点的灵活应用.

练习册系列答案
相关题目
下面数中小于-3的数是( )
| A、-2 | B、4 | C、-4 | D、0 |
某服装店进一批服装,按进价提高20%出售,由于卖不出去,又打八折出售,卖完后服装店是( )
| A、赚了 | B、亏了 |
| C、不赚不亏 | D、都不是 |