题目内容
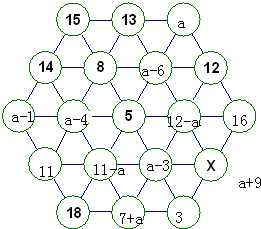
 据说美国有一位铁路职工花了50余年的业余时间,研究得到了一个六角形幻方,如图所示的每一个圆中分别填写了1、2、…、19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x=
据说美国有一位铁路职工花了50余年的业余时间,研究得到了一个六角形幻方,如图所示的每一个圆中分别填写了1、2、…、19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x=19
19
.分析:假设最右上角的空白处是a,则15+13+a=a+12+最右边的数字,得到最右边的数字是16,根据最左边的两边共有一个数字,及和相等,得到左下方的数字是14+15-18=11,然后根据各边的数字和相等是28+a,都用a表示出来,如下图所示;因为这些数字是1到19之间的数字,可以猜出a小于11,大于6,8已经有了,若是9,9-4=5,5早有了,若为7,12-7=5,不可,a只能是10;因此得解.
解答:解:10+9=19;
答:现在已知该图中七个圆内的数字,则图中X=19.
故答案为:19.

答:现在已知该图中七个圆内的数字,则图中X=19.
故答案为:19.
点评:此题考查了凑数谜,假设出未知数a,是解决此题的关键,逐个空求出或用a来表示,最后凑数,得到a的值,从而求出x.

练习册系列答案
相关题目