题目内容
3.$\frac{5}{6}$×$\frac{1}{5}$=$\frac{1}{6}$;$\frac{9}{10}$÷$\frac{3}{5}$=$\frac{3}{2}$;
$\frac{1}{2}$÷$\frac{5}{4}$=$\frac{2}{5}$.
分析 ①已知一个因数和积,求另一个因数用除法计算得解;
②等式两边同时乘$\frac{3}{5}$,计算得解;
③除数=被除数÷商,即$\frac{1}{2}$$÷\frac{2}{5}$,计算得解.
解答 解:①$\frac{1}{6}$÷$\frac{5}{6}$=$\frac{1}{5}$
所以$\frac{5}{6}$×$\frac{1}{5}$=$\frac{1}{6}$;
②$\frac{3}{2}$×$\frac{3}{5}$=$\frac{9}{10}$
所以$\frac{9}{10}$÷$\frac{3}{5}$=$\frac{3}{2}$;
③$\frac{1}{2}$$÷\frac{2}{5}$
=$\frac{1}{2}$×$\frac{5}{2}$
=$\frac{5}{4}$
所以$\frac{1}{2}$÷$\frac{5}{4}$=$\frac{2}{5}$;
故答案为:$\frac{1}{5}$,$\frac{9}{10}$,$\frac{5}{4}$.
点评 把空白处看做要求的未知数,利用等式的性质来解决问题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14.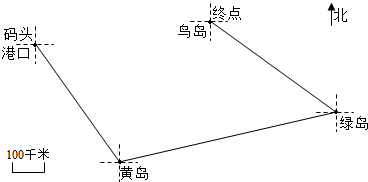 航海路线图.
航海路线图.
根据上面的航海路线图,说一说科学家考察船去时所走的方向和路程.完成下表.
(1)考察船的平均速度是多少?
(2)鸟岛在码头港口的什么方向?相距多远?
(3)有一艘客船在码头港口的北偏东60°相距50千米,在图中标出客船的位置.
 航海路线图.
航海路线图.根据上面的航海路线图,说一说科学家考察船去时所走的方向和路程.完成下表.
| 地址 | 方向 | 路程(千米) | 时间(时) |
| 码头-黄岛 | 东偏南55° | 300 | 20 |
| 黄岛-绿岛 | 北偏东72° | 500 | 40 |
| 绿岛-鸟岛 | 西偏北37° | 300 | 25 |
| 全程 | ____ | 1100 | 85 |
(2)鸟岛在码头港口的什么方向?相距多远?
(3)有一艘客船在码头港口的北偏东60°相距50千米,在图中标出客船的位置.
13.a和b的最大公因数只有1,则a和b的最小公倍数是( )
| A. | a | B. | b | C. | ab | D. | 1 |