题目内容
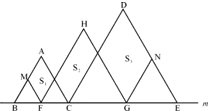 在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知CE=2BC,F、G分别是BC、CE的中点,FM平行于AC,GN平行于DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=________.
在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知CE=2BC,F、G分别是BC、CE的中点,FM平行于AC,GN平行于DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=________.
4
分析:根据题意,可以证明S2与S1两个平行四边形的高相等,长是S1的2倍,S3与S2的长相等,高是S3的一半,这样就可以把S1和S3用S2来表示,从而计算出S2的值.
解答:根据正三角形的性质,∠ABC=∠HFG=∠DCE=60°
∴AB∥HF∥DC∥GN,
设AC与FH交于P,CD与HG交于Q,
∴△PFC、△QCG和△NGE是正三角形,
∵F、G分别是BC、CE的中点
∴BF=MF= AC=
AC= BC,CP=PF=
BC,CP=PF= AB=
AB= BC
BC
∴CP=MF,CQ=BC,QG=GC=CQ=AB,
∴S1= S2,S3=2S2,
S2,S3=2S2,
∵S1+S3=10
∴ S2+2S2=10
S2+2S2=10
∴S2=4.
故答案为4.
点评:此题主要考查了等边三角形的性质及平行四边形的面积求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a?h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.
分析:根据题意,可以证明S2与S1两个平行四边形的高相等,长是S1的2倍,S3与S2的长相等,高是S3的一半,这样就可以把S1和S3用S2来表示,从而计算出S2的值.
解答:根据正三角形的性质,∠ABC=∠HFG=∠DCE=60°
∴AB∥HF∥DC∥GN,
设AC与FH交于P,CD与HG交于Q,
∴△PFC、△QCG和△NGE是正三角形,
∵F、G分别是BC、CE的中点
∴BF=MF=
 AC=
AC= BC,CP=PF=
BC,CP=PF= AB=
AB= BC
BC∴CP=MF,CQ=BC,QG=GC=CQ=AB,
∴S1=
 S2,S3=2S2,
S2,S3=2S2,∵S1+S3=10
∴
 S2+2S2=10
S2+2S2=10∴S2=4.
故答案为4.
点评:此题主要考查了等边三角形的性质及平行四边形的面积求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a?h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
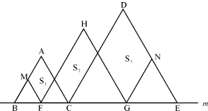 在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知CE=2BC,F、G分别是BC、CE的中点,FM平行于AC,GN平行于DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=
在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知CE=2BC,F、G分别是BC、CE的中点,FM平行于AC,GN平行于DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=