题目内容
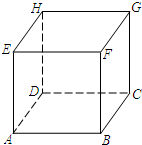 如图,在长方体ABCD-EFGH中,棱AB与棱HG的位置关系是
如图,在长方体ABCD-EFGH中,棱AB与棱HG的位置关系是平行
平行
.棱AD与面DCGH的位置关系是垂直
垂直
.面ABCD与面ADHE的位置关系是垂直
垂直
.分析:(1)因为AB∥EF,HG∥EF,根据平行与同一直线的两条直线互相平行,得出答案;
(2)AD⊥CD,AD⊥HD,而HD与CD在同一平面内,根据直线与平面的判定定理,即可做出判断;
(3)同(2)先证明AB垂直面ADHE,而AB在平面ABCD中,根据两个平面垂直的判断定理,得出答案.
(2)AD⊥CD,AD⊥HD,而HD与CD在同一平面内,根据直线与平面的判定定理,即可做出判断;
(3)同(2)先证明AB垂直面ADHE,而AB在平面ABCD中,根据两个平面垂直的判断定理,得出答案.
解答:解:(1)因为AB∥EF,HG∥EF,
所以AB∥HG,
(2)AD⊥CD,AD⊥HD,而HD与CD在同一平面内,
所以AD⊥面DCGH;
(3)因为AB⊥AE,AB⊥AD,
而AB在平面ABCD中,
所以面ABCD⊥面ADHE;
故答案为:平行;垂直;垂直.
所以AB∥HG,
(2)AD⊥CD,AD⊥HD,而HD与CD在同一平面内,
所以AD⊥面DCGH;
(3)因为AB⊥AE,AB⊥AD,
而AB在平面ABCD中,
所以面ABCD⊥面ADHE;
故答案为:平行;垂直;垂直.
点评:本题用到的知识点:平行与同一直线的两条直线互相平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与这个面垂直;如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂.

练习册系列答案
相关题目
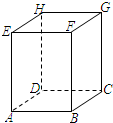 如图,在长方体ABCD-EFGH中,与棱BC异面棱共有
如图,在长方体ABCD-EFGH中,与棱BC异面棱共有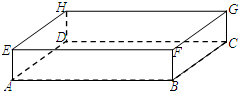 如图,在长方体ABCD-EFGH中,
如图,在长方体ABCD-EFGH中, 如图,在长方体ABCD-EFGH中,与面ADHE平行的面是
如图,在长方体ABCD-EFGH中,与面ADHE平行的面是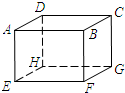 如图,在长方体ABCD-EFGH中,有
如图,在长方体ABCD-EFGH中,有