题目内容
4.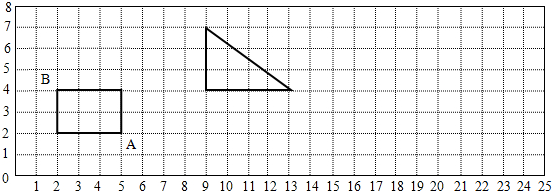
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形,旋转后,B点的位置用数对表示是(7,5).
(2)按1:2画出三角形缩小后的图形.缩小后的面积是原来的$\frac{()}{()}$.
(3)如果1个小方格的面积为1cm2,请你在方格纸上设计一个面积是10cm2的轴对称图形.
分析 (1)根据旋转的特征,长文形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;根据旋转后点B的位置及用数对表示点位置的方法第一个数字表示列数,第二个数字表示行数,即可用数对表示出点B的位置.
(2)图中三角形是两直角边分别为3格、4格的直角三角形,根据图形放大与缩小的意义,按1:2缩小后的三角形是两直角边分别为1.5格、2格的直角三角形,分别求缩小后的三角形面积与原三角形的面积,用缩小后的三角形面积除以原三角形的面积.
(3)根据轴对图形的特征及多边形的面积计算方法,可画一个底为5格,高为4格的等腰三角形,其面积是5×4÷2=10(cm2).
解答 解:(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形(图中红色部分),旋转后,B点的位置用数对表示是(7,5).
(2)按1:2画出三角形缩小后的图形(图中绿色部分).
缩小后的面积是原来的:
(1.5×2÷2)÷(3×4÷2)
=1.5÷6
=$\frac{1}{4}$.
(3)如果1个小方格的面积为1cm2,请你在方格纸上设计一个面积是10cm2的轴对称图形(图中蓝色部分).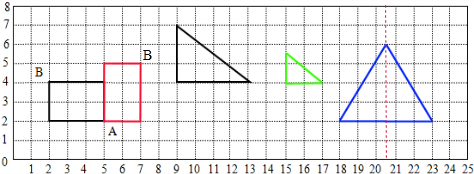
故答案为:7,5,$\frac{1}{4}$.
点评 此题考查的知识点较多,有:作旋转一定度数后的图形、点与数对、图形的放大与缩小、三角形面积的计算、分数的意义、轴对称图形的意义等.

练习册系列答案
相关题目
14.在仓库里有一堆正方体纸箱,从三个不同方位看到的图形如下,这堆纸箱最多有( )个.

| A. | 4 | B. | 7 | C. | 10 | D. | 15 |
16.某商场2014年下半年空调、取暖器销售情况统计表
2015年1月
(1)根据表中的数据,完成下面的统计图.
如图为某商场2015年下半年空调、取暖器销售情况统计图
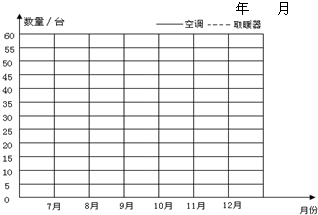
(2)折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量变化的情况.
(3)下半年,取暖器的出售量呈上升趋势,一共出售106台.8月,空调出售的最多.
(4)8月,空调和取暖器的销售量相差最大;11月,空调和取暖器的销售量相差最小.
2015年1月
| 月份 数量/台 商品 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
| 空调 | 58 | 60 | 46 | 30 | 20 | 12 |
| 取暖器 | 8 | 5 | 10 | 15 | 30 | 48 |
如图为某商场2015年下半年空调、取暖器销售情况统计图

(2)折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量变化的情况.
(3)下半年,取暖器的出售量呈上升趋势,一共出售106台.8月,空调出售的最多.
(4)8月,空调和取暖器的销售量相差最大;11月,空调和取暖器的销售量相差最小.
14.下列数量中,与1.30米相等的是( )
| A. | 13分米 | B. | 130厘米 | C. | 1米30厘米 |

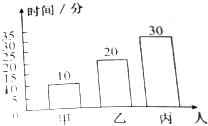 图中表示甲乙丙三人单独完成一篇1500字文稿的打字任务所需要的时间.
图中表示甲乙丙三人单独完成一篇1500字文稿的打字任务所需要的时间.