题目内容
19.一名物流公司的快递员,每天他从物流公司装好货物后,一直在一条南北走向的公路上送快件,假若物流公司记为原点,向南走1千米记为“+1”,向北走1千米记为“-1”,这名快递员某一天具体行程如下:+12,+11,-26,-6,-18,+7
(1)快递员走完以上行程后在物流公司的什么位置?
(2)如果快递员所开的车100千米耗油7.5升,那他走完以上行程耗油多少升?
(3)快递员走完以上行程后以60千米/小时的速度开车回公司,走到立交桥时接到公司电话,让他尽快赶回去,快递员便以80千米/小时的速度赶了回去,结果提前了3分钟,问:物流公司与立交桥距离多少千米?
分析 (1)根据有理数的加法,要求这名快递员某一天具体行程,列式为12+11+(-26)+(-6)+(-18)+7,计算可得答案;
(2)根据单位耗油量乘以路程等于总耗油量,可得答案;
(3)根据提速前的时间减去提速后的时间等于节省的时间,可得方程,然后解方程,可得答案.
解答 解:(1)12+11+(-26)+(-6)+(-18)+7=-20(千米).
答:这个快递员走完以上行程后在物流公司北20千米.
(2)(12+11+|-26|+|-6|+|-18|+7)÷100×7.5
=80÷100×7.5
=6(升)
答:他走完以上行程耗油6升.
(2)设物流公司与立交桥距离x千米,根据题意,得
$\frac{x}{60}$-$\frac{x}{80}$=3÷60
$\frac{4x}{240}$-$\frac{3x}{240}$=$\frac{12}{240}$
$\frac{x}{240}$=$\frac{12}{240}$
x=12
答:物流公司与立交桥距离12千米.
点评 本题考查了正数和负数,利用了有理数的加法运算,找出提速前的时间减去提速后的时间等于节省的时间的等量关系是解题关键.

练习册系列答案
相关题目
10.等腰三角形的两边长分别是4cm和2cm,则这个三角形的周长是( )
| A. | 10cm | B. | 8cm | C. | 10cm或8cm |
8.甲、乙两袋米,已知甲的$\frac{1}{3}$和乙的$\frac{1}{2}$同样多,那么甲、乙两袋米的关系是( )
| A. | 甲比乙多 | B. | 甲比乙少 | C. | 不能判断 |
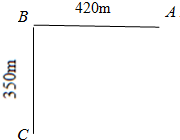 装路灯(如图所示),街道ABC在B处拐弯,在街道的一侧等距离装上路灯,要在A,B,C处各装一盏路灯,这个街道至少要装上多少盏路灯.
装路灯(如图所示),街道ABC在B处拐弯,在街道的一侧等距离装上路灯,要在A,B,C处各装一盏路灯,这个街道至少要装上多少盏路灯.