题目内容
4.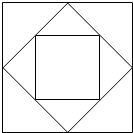 如图,正中的正方形面积是1平方厘米,外面两个正方形的面积分别是2平方厘米和4平方厘米.
如图,正中的正方形面积是1平方厘米,外面两个正方形的面积分别是2平方厘米和4平方厘米.
分析 如图,通过添加辅助线,把正中正方形和中间正方形都平均分成2份,即把中间的正方形分成了两个同样的长方形,正中的正方形分成了两个同样的三角形,设中间正方形的边长一个数值,即可求出被分成的长方形与三角形的面积的比,从求出当正中正方形面积与是间正方形面积的比,进而求出中间正方形的面积;同理,中间正方形的面积与最外正方形面积的比也是这个比,据此再求出最外正方形的面积.
解答 解:如图,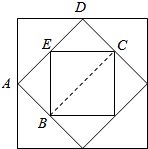
连结BC,则三角形EBC是正中正方形面积的一半,长方形ABCD是中间正方形面积的一半,
设中间长方形的长为2,则宽为1,
长方形ABCD面积是2×1=2,
三角形EBC的面积是2×1÷2=1,
三角形EBC的面积占长方形ABC面积的$\frac{1}{2}$,
即中间正方形面积是正中正方形面积的2倍,
因此,是间正方形的面积是1×2=2(平方厘米);
同理,最外正方形面积是中间正方形面积的2倍,
即最外正方形面积是2×2=4(平方厘米).
故答案为:2,4.
点评 如果按正常思路,由正中正方形面积求它的边长,再根据勾股定理求出是间正方形的边长,再求出它的面积,同理再求最外正方形的面积,比较麻烦,且用小学知识不易解答.此题通过巧妙地添加一辅助线,求出正中正方形与中间正方形面积的比,求出中间正方形的面积,同理求出最外正方形的面积,就比较容易了.

练习册系列答案
相关题目
14.方程0.5x=2的解是( )
| A. | x=0.25 | B. | x=1 | C. | x=4 |