题目内容
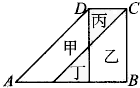
 图中ABCD是平行四边形,AD=20厘米,求图中阴影部分的面积.
图中ABCD是平行四边形,AD=20厘米,求图中阴影部分的面积.
解:ABCD是平行四边形,AD∥BC,BO⊥AD,则BO⊥BC,BC是圆的切线,所以BO是圆的半径,O是圆心,因此AO=BO=DO= AD=10厘米,
AD=10厘米,
S?ABCD=AD?BO=200(平方厘米),
S△AOB= AO?BO=50(平方厘米),
AO?BO=50(平方厘米),
所以,阴影部分的面积=S?ABCD+ S⊙O-2(S△AOB+
S⊙O-2(S△AOB+ S⊙O)=S?ABCD-2S△AOB=200-2×50=100(平方厘米);
S⊙O)=S?ABCD-2S△AOB=200-2×50=100(平方厘米);
答:图中阴影部分的面积是100平方厘米.
分析:把图形画的规范后,如下图所示,,则圆的直径是AD,半径是10厘米,过B点做AD的垂线,垂足为O,因为?ABCD中BC∥AD,BC是圆的切线,所以BO⊥BC,所以O是圆心,OB、OA、OD都是圆的半径,BO= AD=10厘米,通过观察,发现:阴影部分的面积=?ABCD的面积+半圆的面积-2[△AOB的面积+
AD=10厘米,通过观察,发现:阴影部分的面积=?ABCD的面积+半圆的面积-2[△AOB的面积+ 圆(扇形BOD)的面积],代入数值,即可得解.
圆(扇形BOD)的面积],代入数值,即可得解.

点评:此题考查了组合图形的面积,关键是看出O是圆心,BO、AO、DO是半径,最后看出平行四边形面积加上半圆面积等于阴影部分面积加上两倍的空白部分面积,通过整理,阴影部分面积就等于平行四边形面积减去2倍的三角形AOB面积,是最巧妙之处.
 AD=10厘米,
AD=10厘米,S?ABCD=AD?BO=200(平方厘米),
S△AOB=
 AO?BO=50(平方厘米),
AO?BO=50(平方厘米),所以,阴影部分的面积=S?ABCD+
 S⊙O-2(S△AOB+
S⊙O-2(S△AOB+ S⊙O)=S?ABCD-2S△AOB=200-2×50=100(平方厘米);
S⊙O)=S?ABCD-2S△AOB=200-2×50=100(平方厘米);答:图中阴影部分的面积是100平方厘米.
分析:把图形画的规范后,如下图所示,,则圆的直径是AD,半径是10厘米,过B点做AD的垂线,垂足为O,因为?ABCD中BC∥AD,BC是圆的切线,所以BO⊥BC,所以O是圆心,OB、OA、OD都是圆的半径,BO=
 AD=10厘米,通过观察,发现:阴影部分的面积=?ABCD的面积+半圆的面积-2[△AOB的面积+
AD=10厘米,通过观察,发现:阴影部分的面积=?ABCD的面积+半圆的面积-2[△AOB的面积+ 圆(扇形BOD)的面积],代入数值,即可得解.
圆(扇形BOD)的面积],代入数值,即可得解.
点评:此题考查了组合图形的面积,关键是看出O是圆心,BO、AO、DO是半径,最后看出平行四边形面积加上半圆面积等于阴影部分面积加上两倍的空白部分面积,通过整理,阴影部分面积就等于平行四边形面积减去2倍的三角形AOB面积,是最巧妙之处.

练习册系列答案
相关题目