题目内容
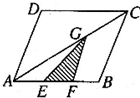 在平行四边形ABCD中,AE=EF=FB.AG=2CG,三角形GEF的面积是6平方厘米,平行四边形的面积是多少平方厘米?
在平行四边形ABCD中,AE=EF=FB.AG=2CG,三角形GEF的面积是6平方厘米,平行四边形的面积是多少平方厘米?分析:如下图:连接BG,设△ABC以BC为底边的高为H,△EFG以FG为底边的高为h;因为AC:AG=AB:AF=2:3,所以FG∥BC,所以△ABC∽△AFG,所以FG:BC=2:3,即BC=
FG,因为AE=EF=FB,所以h:H=
,即H=3h,由此求出三角形ABC的面积,进而求出平行四边形的面积.
| 3 |
| 2 |
| 1 |
| 3 |

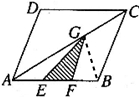
解答:解:设△ABC以BC为底边的高为H,△EFG以FG为底边的高为h;
因为AC:AG=AB:AF=2:3
所以FG∥BC
所以△ABC∽△AFG
所以FG:BC=2:3,即BC=
FG
因为AE=EF=FB
所以h:H=
,即H=3h
因为三角形EFG的面积=FG×h÷2=6(平方厘米)
所以三角形ABC的面积=BC×H÷2=
FGX3h÷2=
×(FG×h÷2)=27(平方厘米)
所以平行四边形ABCD的面积=2个三角形ABC的面积=54(平方厘米);
答:平行四边形的面积是54平方厘米.
因为AC:AG=AB:AF=2:3
所以FG∥BC
所以△ABC∽△AFG
所以FG:BC=2:3,即BC=
| 3 |
| 2 |
因为AE=EF=FB
所以h:H=
| 1 |
| 3 |
因为三角形EFG的面积=FG×h÷2=6(平方厘米)
所以三角形ABC的面积=BC×H÷2=
| 3 |
| 2 |
| 9 |
| 2 |
所以平行四边形ABCD的面积=2个三角形ABC的面积=54(平方厘米);
答:平行四边形的面积是54平方厘米.
点评:解答本题的关键是利用相似三角形的相似比求出三角形ABC的面积.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
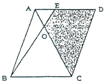 如右图,在平行四边形ABCD中OE:0B=1:3,三角形AOB的面积是30平方厘米.求阴影部分的面积是多少平方厘米.
如右图,在平行四边形ABCD中OE:0B=1:3,三角形AOB的面积是30平方厘米.求阴影部分的面积是多少平方厘米. 在平行四边形ABCD中,已知∠A=70°,求其他3个角的度数.∠A=70°∠B=
在平行四边形ABCD中,已知∠A=70°,求其他3个角的度数.∠A=70°∠B= (2010?深圳模拟)如图,在平行四边形ABCD中,AE=
(2010?深圳模拟)如图,在平行四边形ABCD中,AE= 如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是
如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是