题目内容
(2012?郑州模拟)如图,有A、B、C三种型号的塑料板.已知A型板有30块,要购买B、C两种型号的塑料板若干?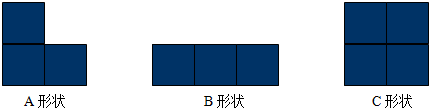
(1)拼成1个4×4的正方形有几种方法?每种方法需要三种型号的塑料板各多少块?试着画出每种拼法的草图(数量一样的算一种拼法)
(2)拼成10个4×4的正方形,A型版要全部用上,若B型板每块价格为5元,C型板每块价格为4元,问应该购买B、C两种型号的塑料板各多少个,才能使所花的钱尽可能划算?最低需要多少钱?

(1)拼成1个4×4的正方形有几种方法?每种方法需要三种型号的塑料板各多少块?试着画出每种拼法的草图(数量一样的算一种拼法)

(2)拼成10个4×4的正方形,A型版要全部用上,若B型板每块价格为5元,C型板每块价格为4元,问应该购买B、C两种型号的塑料板各多少个,才能使所花的钱尽可能划算?最低需要多少钱?
分析:(1)要拼成1个4×4的正方形,它用16个格子,就要用这三种型号的塑料板组合起来得是16,方法一:用4个C形状的;方法二:3个A形状的,1个B形状的,1个C形状的;方法三:1个A形状的,3个B形状的,1个C形状的.方法四:4个A形状的,1个C形状的.
(2)要使A型板全用上,且花钱划算,就要多买C型板;根据上面的拼法:A型板全用完,就要用方法三和方法四结合用,据此解答.
(2)要使A型板全用上,且花钱划算,就要多买C型板;根据上面的拼法:A型板全用完,就要用方法三和方法四结合用,据此解答.
解答:解:(1)要拼成1个4×4的正方形,它用16个格子,就要用这三种型号的塑料板组合起来得是16,方法一:用4个C形状的;方法二:3个A形状的,1个B形状的,1个C形状的;方法三:1个A形状的,3个B形状的,1个C形状的.方法四:4个A形状的,1个C形状的;画图如下:
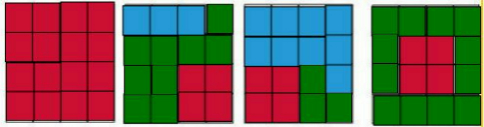 ;
;
(2)30个A型板用方法四需要用小正方形的个数是:30÷4=7(个)…2(块),
余下的两块A型板,用方法三需要小正方形的个数是:2÷1=2(个),
故B型板的个数是:3×2=6(个),
2个方法三中需C型板的个数是:2×1=2(个),
7个方法四中需C型板的个数是:7×1=7(个),
剩余的用方法一需C型板的个数是;4×1=4(个),
共需C型板的个数是:2+7+4=13(个),
C型板的钱数是:13×4=52(元);
B型板的钱数是:6×5=30(元),
一共需要的钱数是:52+30=82(元).
答:应该购买B型板6个,C型形板13个,最低要用82元.
 ;
;(2)30个A型板用方法四需要用小正方形的个数是:30÷4=7(个)…2(块),
余下的两块A型板,用方法三需要小正方形的个数是:2÷1=2(个),
故B型板的个数是:3×2=6(个),
2个方法三中需C型板的个数是:2×1=2(个),
7个方法四中需C型板的个数是:7×1=7(个),
剩余的用方法一需C型板的个数是;4×1=4(个),
共需C型板的个数是:2+7+4=13(个),
C型板的钱数是:13×4=52(元);
B型板的钱数是:6×5=30(元),
一共需要的钱数是:52+30=82(元).
答:应该购买B型板6个,C型形板13个,最低要用82元.
点评:本题考查了学生对于图形组合的能力,以及怎样在这些拼组中选择最经济的方法.

练习册系列答案
相关题目
 (2012?郑州模拟)如图所示的四个圆形跑道,每个跑道的长都是1千米,A、B、C、D四位运动员同时从交点O出发,分别沿四个跑道跑步,他们的速度分别是每小时4千米,每小时8千米,每小时6千米,每小时12千米.问从出发到四人再次相遇,四人共跑了多少千米?
(2012?郑州模拟)如图所示的四个圆形跑道,每个跑道的长都是1千米,A、B、C、D四位运动员同时从交点O出发,分别沿四个跑道跑步,他们的速度分别是每小时4千米,每小时8千米,每小时6千米,每小时12千米.问从出发到四人再次相遇,四人共跑了多少千米?