Question

【题目】如图，已知边长为8的正方形ABCD，E为AD的中点，P为CE的中点，△BDP的面积 ．

Answer 1

【答案】8

【解析】

试题分析：连接BE，因为E为AD的中点，则△BEC的面积等于正方形ABCD的面积的一半，又因为P为CE的中点，所以△BPC的面积等于△BEC的面积的一半，根据三角形的面积公式求出三角形CDE的面积，而△CDP的面积等于△CDE的面积的一半，

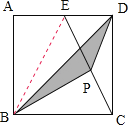
解答：解：连接BE，因为E为AD的中点，

所以△BEC的面积=×正方形ABCD的面积=×8×8=32；

因为P为CE的中点，所以△BPC的面积=×△BEC的面积=16；

△CDE的面积=×8×4=16；

△CDP的面积=×△CDE的面积=×16=8．

而△ABD的面积=×8×8=32．

所以△BDP的面积=正方形ABCD的面积﹣△ABD的面积﹣△BPC的面积﹣△DPC的面积=64﹣32﹣16﹣8=8．

故答案为：8．