Question

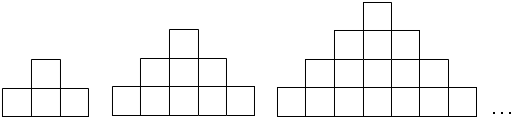
观察如图，寻找规律，并把表格填写完整．（每个小正方形的边长是1厘米）

小正方形的个数	4	9	16	25	…	144
周长（厘米）					…

Answer 1

考点：数与形结合的规律

专题：探索数的规律

分析：第一个图形有2²个小正方形，周长是（3+2）×2=10厘米；第二个图形有3²个，周长是（5+3）×2=16厘米，第三个图形是4²个小正方形，周长是（7+4）×2=22厘米，则第四个图形有5²个小正方形，周长是（9+5）×2=28厘米，…，所以每个图形的周长，经过平移后，都等于它所在的长方形的周长，长方形的长分别是：3、5、7、9、…，宽分别是：2、3、4、5、6…，144=12²，是第11个图形，所以长是23厘米，宽是12厘米，则周长是（23+12）×2=70厘米，据此即可解答问题．

解答： 解：根据题干分析可得：第一个图形有2²个小正方形，周长是（3+2）×2=10厘米；
第二个图形有3²个，周长是（5+3）×2=16厘米，
第三个图形是4²个小正方形，周长是（7+4）×2=22厘米，
则第四个图形有5²个小正方形，周长是（9+5）×2=28厘米，
…，
所以每个图形的周长，经过平移后，都等于它所在的长方形的周长，
长方形的长分别是：3、5、7、9、…，
宽分别是：2、3、4、5、6…，
144=12²，是第11个图形，
所以长是23厘米，宽是12厘米，则周长是（23+12）×2=70厘米，
故完成表格如下：

小正方形的个数	4	9	16	25	…	144
周长（厘米）	10	16	22	28	…	70

点评：主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．