题目内容
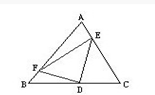 已知:AE=
已知:AE= AC,CD=
AC,CD= BC,BF=
BC,BF= AB,求三角形DEF的面积与三角形ABC的面积之比.
AB,求三角形DEF的面积与三角形ABC的面积之比.
解:因为S△BDF=S△ABC× ×
× =
= S△ABC,
S△ABC,
S△CDE=S△ABC× ×
× =
= S△ABC,
S△ABC,
S△AEF=S△ABC× ×
× =
= S△ABC,
S△ABC,
所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF= S△ABC,
S△ABC,
答:三角形DEF的面积与三角形ABC的面积之比为61:120.
分析:可以先求出边上的3个小三角形与S△ABC的面积之间的关系:S△BDF=S△ABC× ×
× =
= S△ABC,S△CDE=S△ABC×
S△ABC,S△CDE=S△ABC× ×
× =
= S△ABC,S△AEF=S△ABC×
S△ABC,S△AEF=S△ABC× ×
× =
= S△ABC,所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF=
S△ABC,所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF= S△ABC,依此即可求解.
S△ABC,依此即可求解.
点评:考查了三角形面积与底的正比关系,得到边上的3个小三角形与S△ABC的面积之间的关系是解题的难点,本题有一定的难度.
 ×
× =
= S△ABC,
S△ABC,S△CDE=S△ABC×
 ×
× =
= S△ABC,
S△ABC,S△AEF=S△ABC×
 ×
× =
= S△ABC,
S△ABC,所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF=
 S△ABC,
S△ABC,答:三角形DEF的面积与三角形ABC的面积之比为61:120.
分析:可以先求出边上的3个小三角形与S△ABC的面积之间的关系:S△BDF=S△ABC×
 ×
× =
= S△ABC,S△CDE=S△ABC×
S△ABC,S△CDE=S△ABC× ×
× =
= S△ABC,S△AEF=S△ABC×
S△ABC,S△AEF=S△ABC× ×
× =
= S△ABC,所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF=
S△ABC,所以S△DEF=S△ABC-S△BDF-S△CDE-S△AEF= S△ABC,依此即可求解.
S△ABC,依此即可求解.点评:考查了三角形面积与底的正比关系,得到边上的3个小三角形与S△ABC的面积之间的关系是解题的难点,本题有一定的难度.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知AE=
已知AE= AC,FC=
AC,FC=

